The Snowflake Sudoku is composed of hexagons that overlap partially. The goal is to put a number from 1 to 6 in each hexagon so that no number repeats. The problem is that a hexagon shares cells with 2 other hexagons then a number of a hexagon belong to two other hexagons. This is an example of this puzzle with the solution.
Some considerations about the grid.
The grid is composed of 13 hexagons, each hexagon has a circle in the middle.
But also the grid has 6 partial hexagons (shaded in red and yellow) containing 4 cells, then only 4 numbers ( from one to six) can be written in these areas with no repetition.
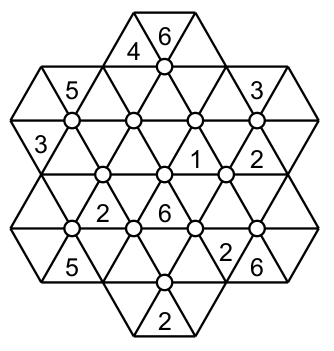
Example of resolution
With this example we are able to start the puzzle like that ( I colored the centre of some hexagons to distinguish them) .
The hexagon having a blue centre intersect two other hexagons with a red center. These two hexagons have a 2 then the only empty cell in the blue hexagon must accept the 2 (the number written in red).This let us add a new number, because the new 2 is part of two hexagons (with the green centre) and the only cell available in the yellow hexagon receive the 2 (again written in red). The consequence is that the second green hexagon has a 1 and the only free cell in the yellow hexagon that do not belong to the second green hexagon receive the 1 (in red). Now look at the black hexagon (at the bottom), the blue hexagon has a 6 and it shares two cells with the black hexagon. But the partial hexagon at the right of the black one has a 6 and it shares two other cells with the black one. So the only cell available has the 6 (in red).
This puzzle could have a bigger size with 43 hexagons and 12 partial hexagons like this.
Comments powered by CComment