- Details
SUDOKUBE
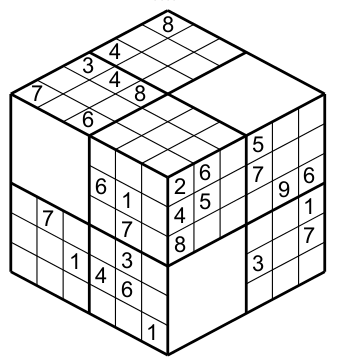
A Sudokube is a 3D Sudoku. A regular Sudoku is composed of nine 3x3 regions, columns and rows. A Sudokube as the same elements ( 9 regions,columns and rows) arranged on a cube instead of a 9x9 grid. The cube has three visible sides, each side has 3 regions. The columns and rows span on two sides (see Figure 1).
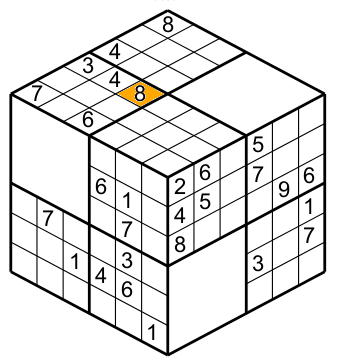
To illustrate how the regions. columns and rows work I show you and example with a specific cell, in figure 2 the orange cell has a 8.
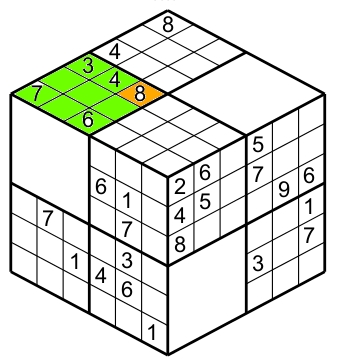
This cell pertains to the green region (figure 3).
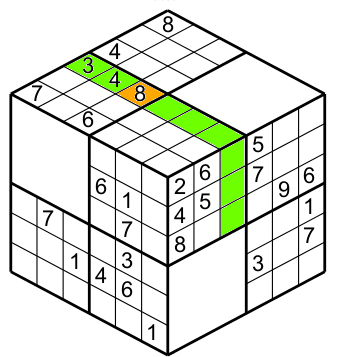
This cell is inside the green row (figure 4).
Also in the green column (note the column overpass the big white square- figure 5).
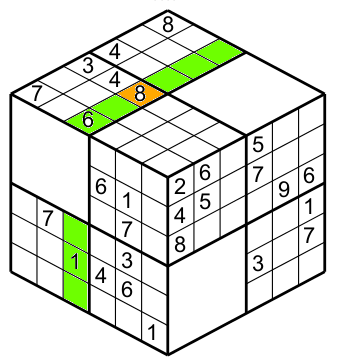
Finally all together (figure 6).
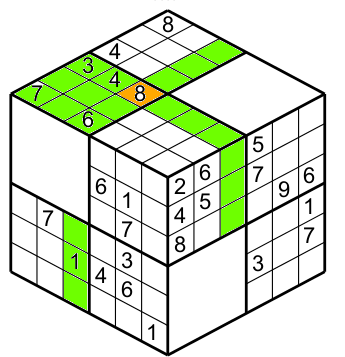
The main difference between a Sudokube and an Sudoku 3D is that the Sudoku 3D has regions (2x4),columns and row containing 8 cells and the Sudokube has regions,columns and rows containing 9 cells as a standard Sudoku.
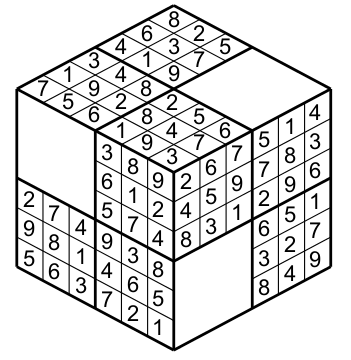
So the rules are the same: put numbers from 1 to 9 in each region, column and row such that each region,column and row has once each number. This is a Sudokube and its solution.

MULTI-SUDOKUBE
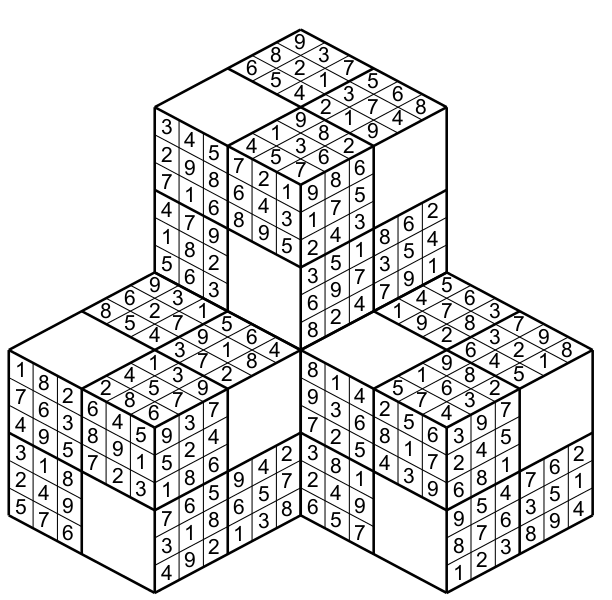
It is possible two combined two or even three cubes together to form a Muti-Sudokube puzzle. An example of a two cubes puzzle (figure 7).

And a three cubes puzzle (figure 8)
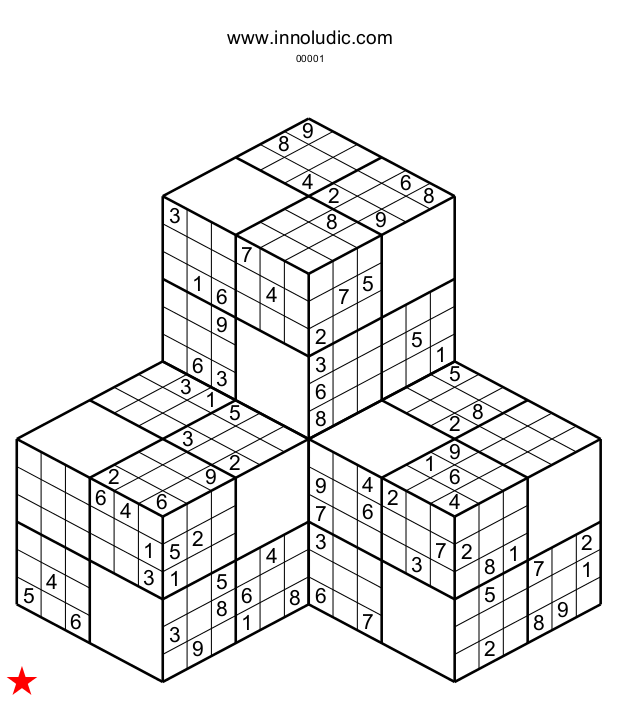
The rules for each cube are the same, but the twist is that when one face of a cube touchs another face of a different cube then these two different faces constitute an suplementary row or column. I explain how with the figure 9.
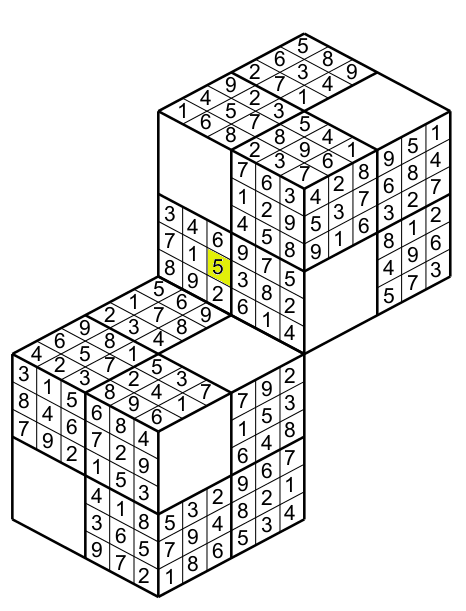
This is a solution of a Muti-Sudokube, first the usual rules apply for each cube, then the yellow cell having a 5 belongs to the region (green cells) figure 10
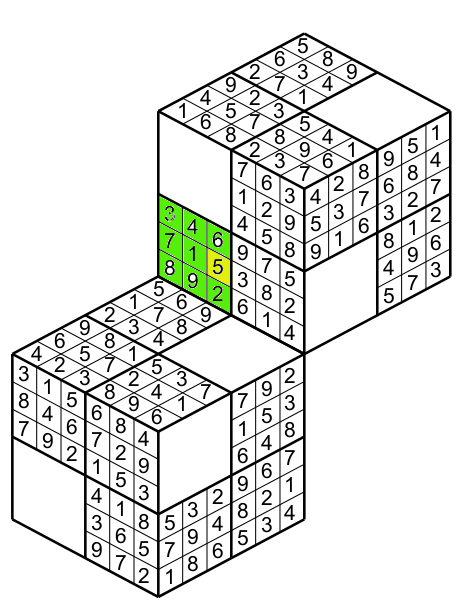
This cell also belong to the green row ( see figure 11)
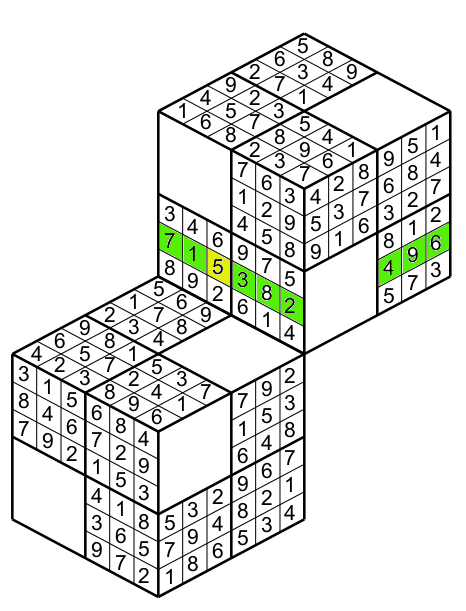
And finaly to the green column (figure 12)
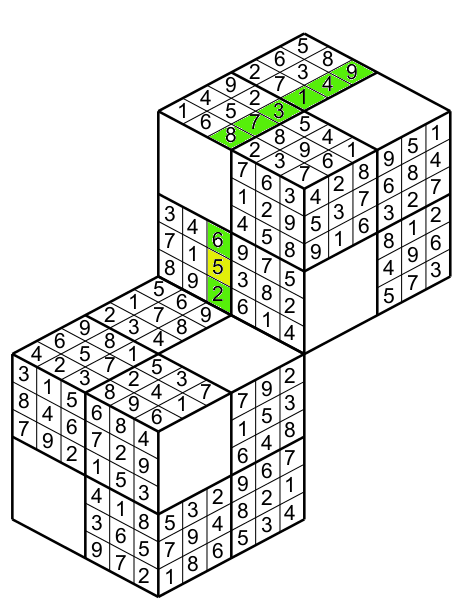
But also because the face having the yellow cell touchs a face belonging to a different cube then these two faces form a new column for the yellow cell (figure 13).
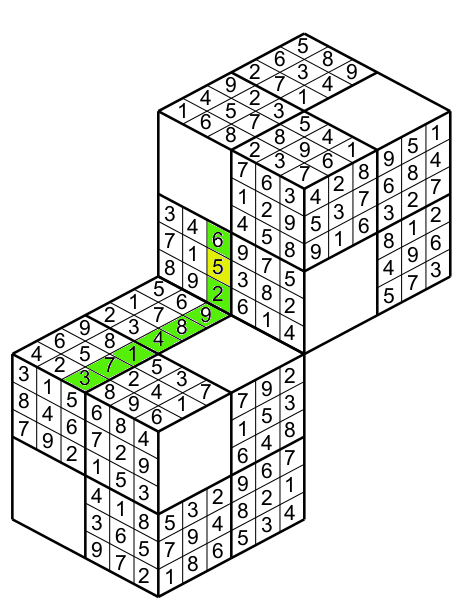
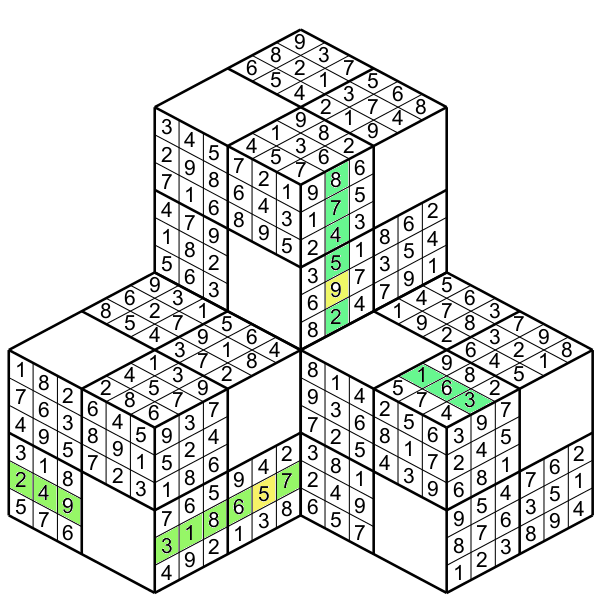
These new particularity will help you to solve the puzzle because you have more information to decide which number to write. In fact you could not only rely on the clues on a cube to determine a number in a cell but also in some occasion you could rely on the clues on another cube. So this aspect compells you to open your horizon to complet this puzzle. When three cubes are together ( figure 14) then each cube touchs to the two another cubes..

This is the solution (figure 15)
By example in figure 16 the yellow cell having a 9 belongs to the green column and row on its cube ( I dont represent the region).
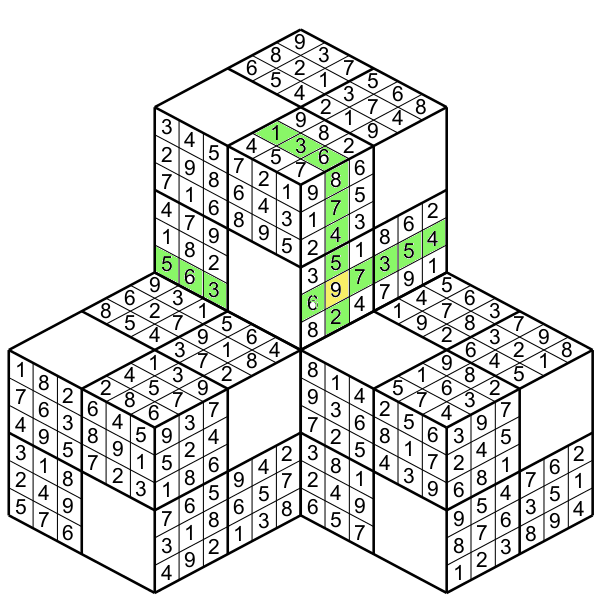
but also to the supplementary column formed by the addition on the other face of the cube touching its face.
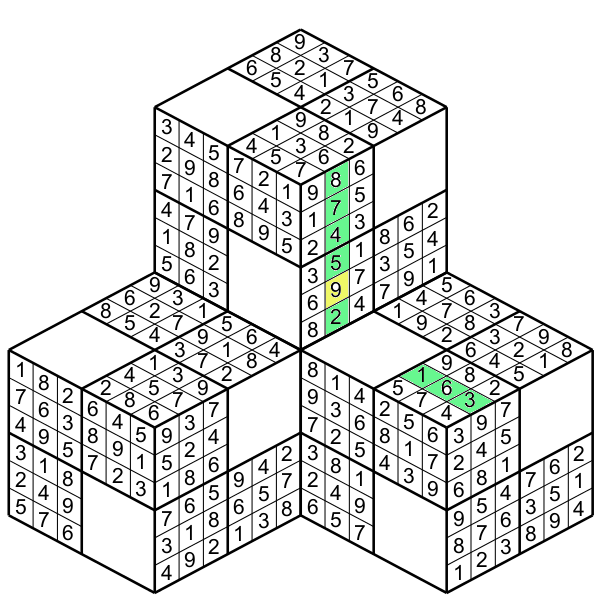
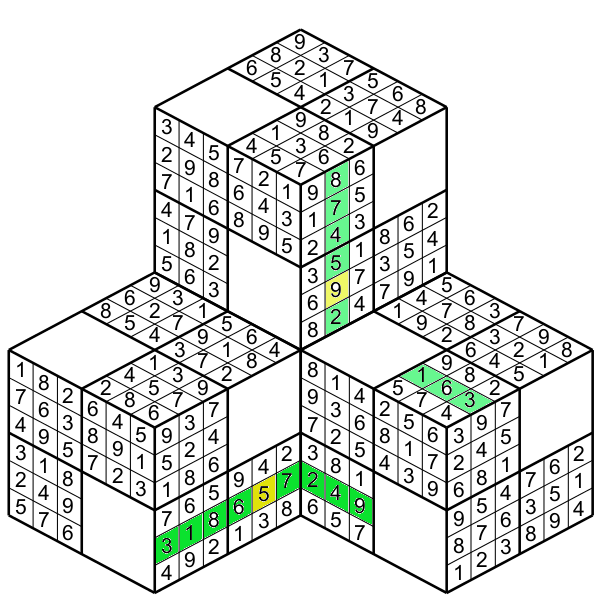
By the same way the other yellow cell having a 5 is not olny pertaining to the row on its cube (green row figure 18)
but also to the new row formed by the addition of the two adjacent faces figure 19.
If you are familar with my Hyper Sudoku 3D puzzles you will recognise the same peculiarity. The best way to appreciate this puzzle is to solve it !
 No comments
No comments















