I present you the Snowflake puzzle, which is a fascinating puzzle, it is a cross between the Snowflake Sudoku and Kakuro. Be cautious we rapidly become an addict to this puzzle.
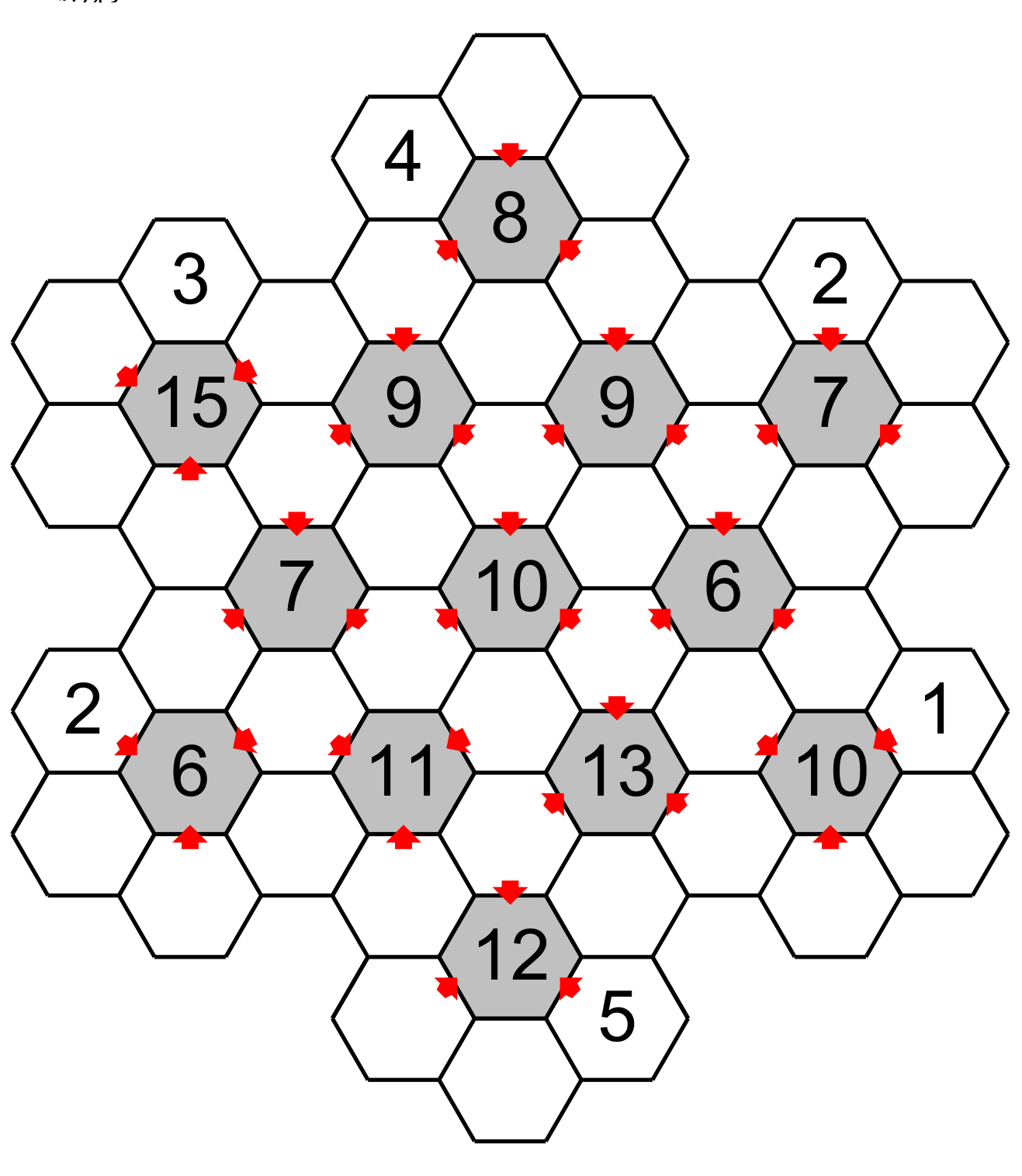
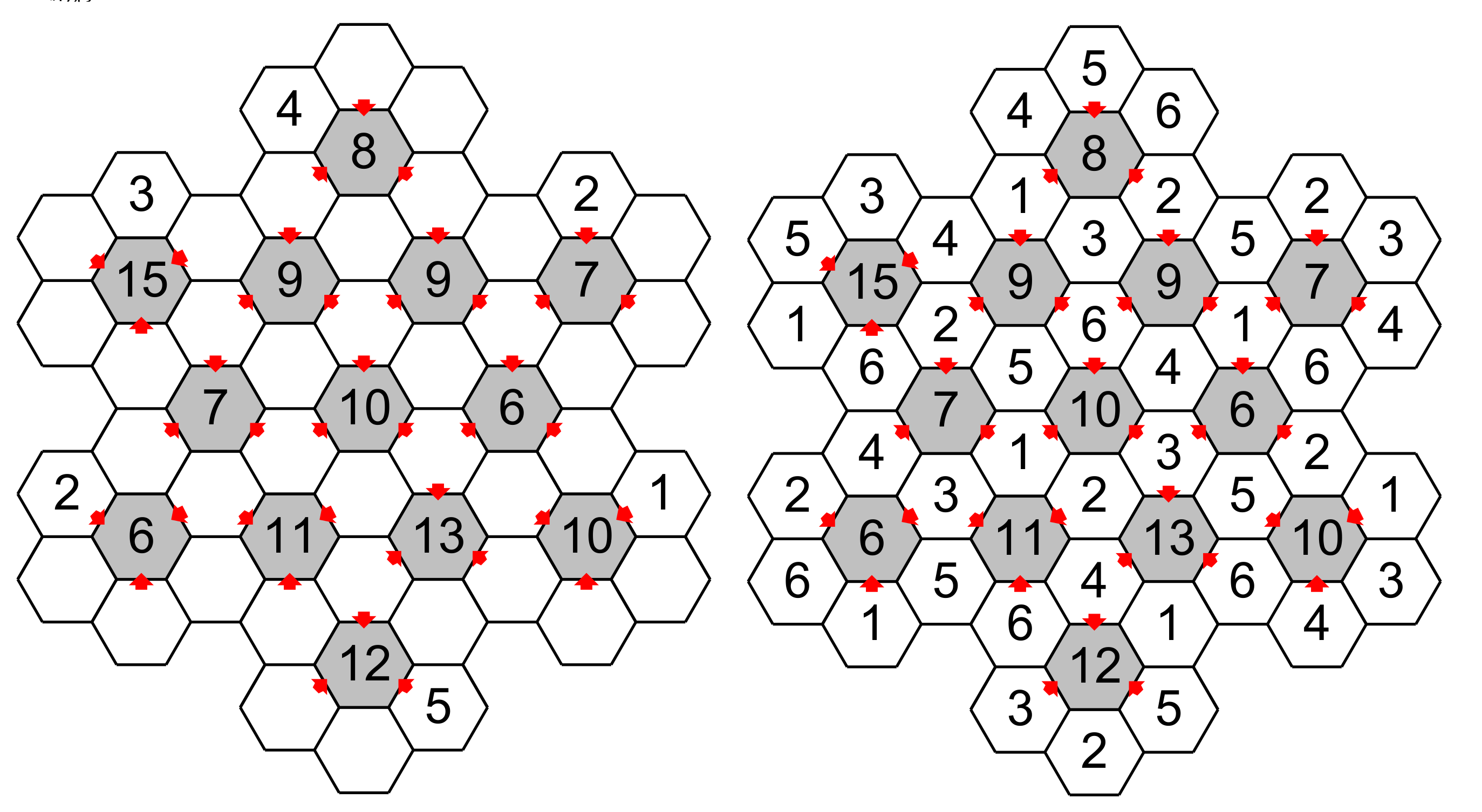
First of all, the Snowflake puzzle is a grid made of hexagons, they are 13 central hexagons (each in gray) surrounded by 6 empty hexagons (in white). The central hexagons contain a number that represents the total of the three white hexagons pointing to them. Each hexagon around the central hexagon must have a number from 1 to 6 without repetition. The goal is to fill all the hexagon. At the beginning some clues are in the empty hexagon.
This is a grid.
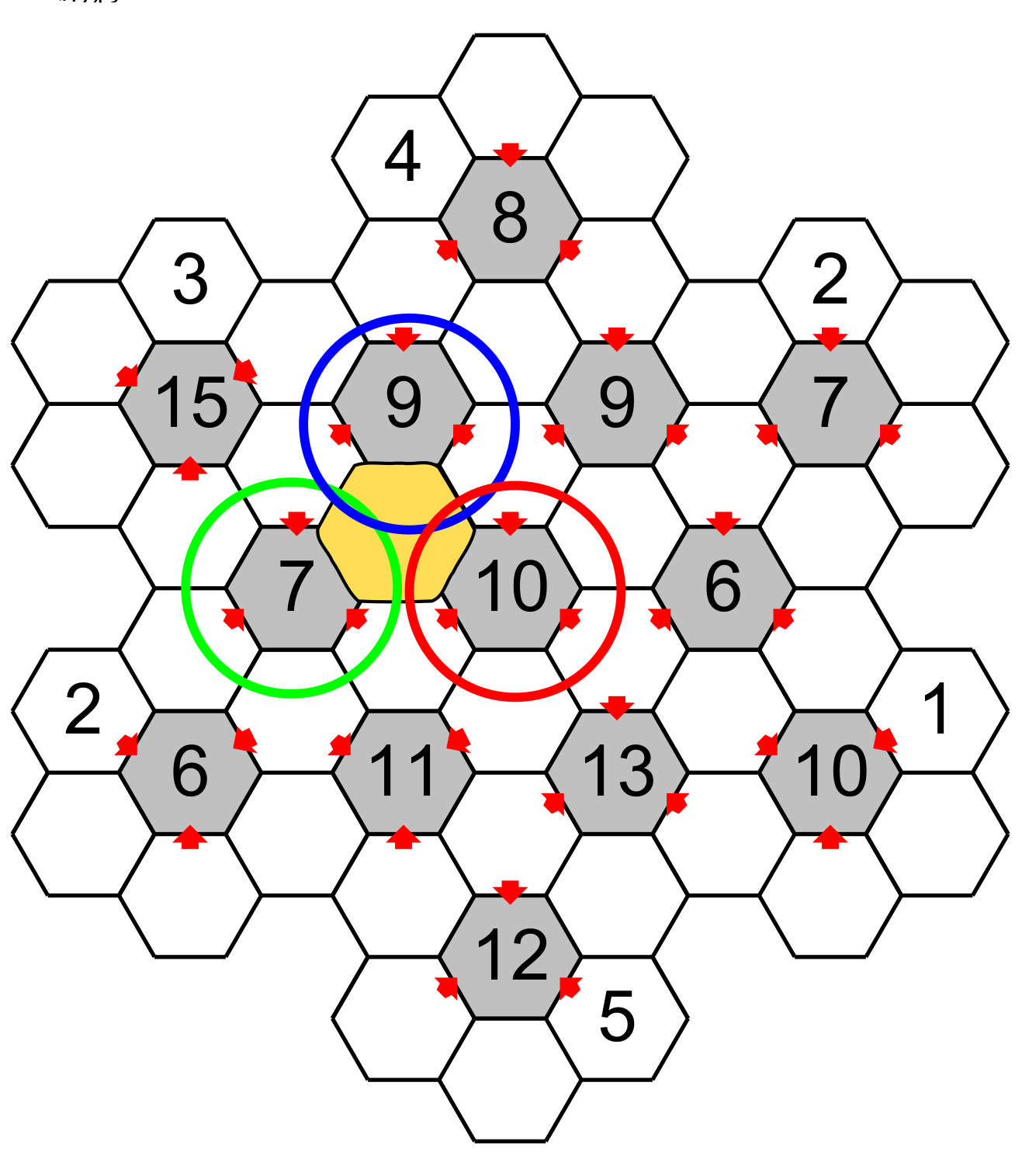
An empty hexagon may be around one, two or three central hexagons. In the following figure, the yellow hexagon is around three central hexagons (blue, yellow and red circle).
As each empty hexagon around a central hexagon must have the numbers 1,2,3,4,5 and 6 then the total of all the numbers around the central hexagon is 21 (1+2+3=4+5+6=21). This peculiarity could help us to solve this puzzle. For example, if we isolate a part of the grid.
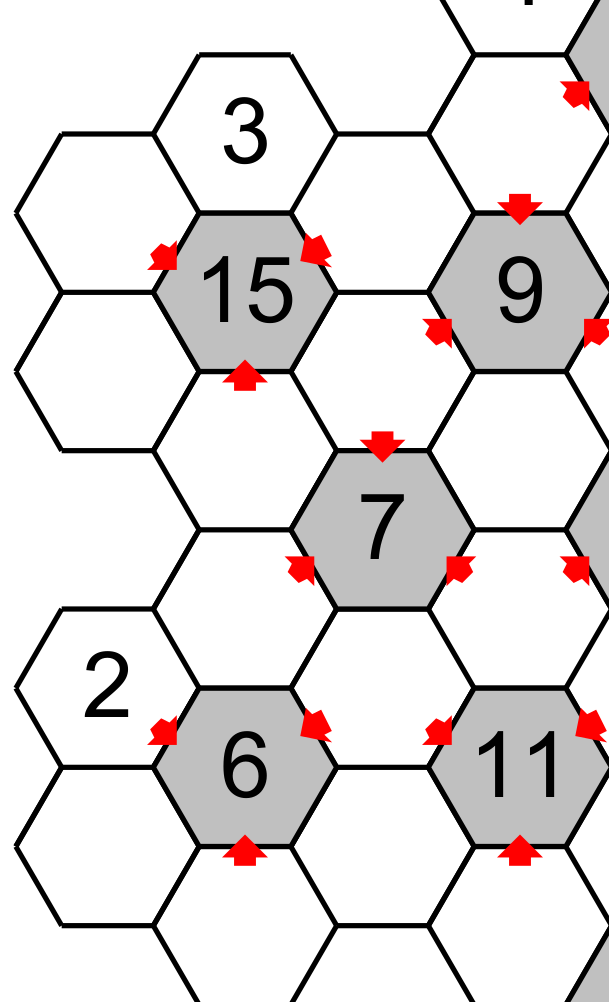
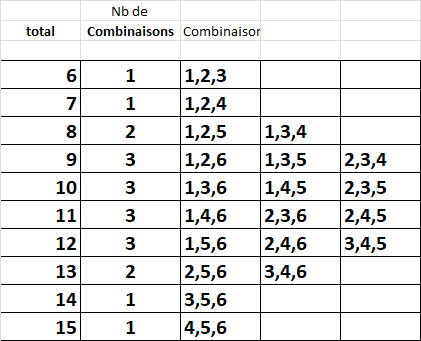
We know that the three hexagons pointing to the central hexagon having 15 have a total of 15. It means that the three other hexagons have a total of 6 (21-15). The totals of 6,7,14 and 15 have only one combination of three different numbers: 6=1+2+2+3, 7=1+2+4, 15=3+5+6 and 15=4+5+6. All the other total (between 7 and 14) have two or three different combinations (see the table at the end ).
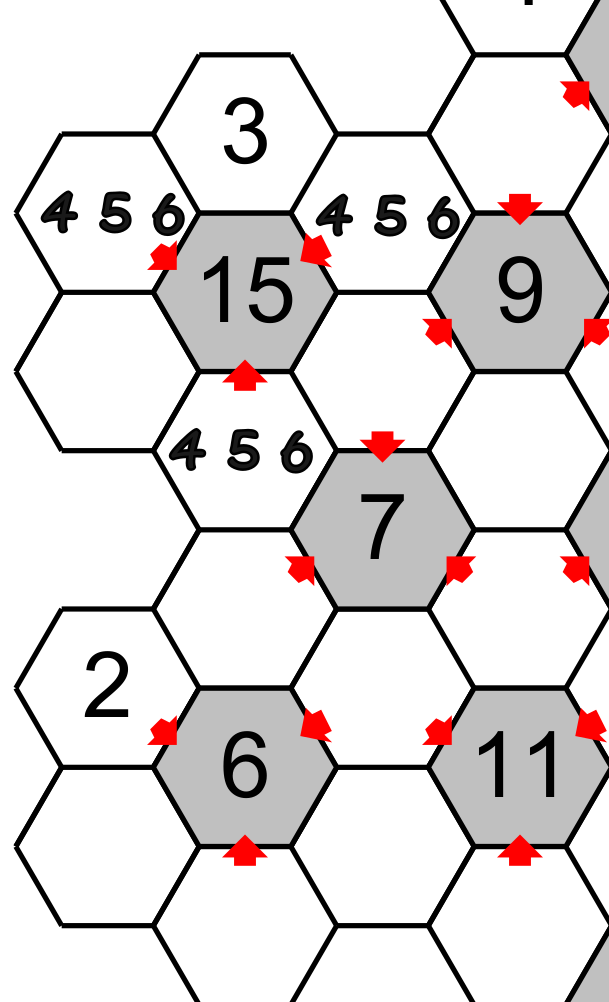
Then the hexagons pointing must have 4,5,6 and the other complementary hexagon must have 1,2,3. Since one hexagon have already a 3 the other will have 1 or 2.
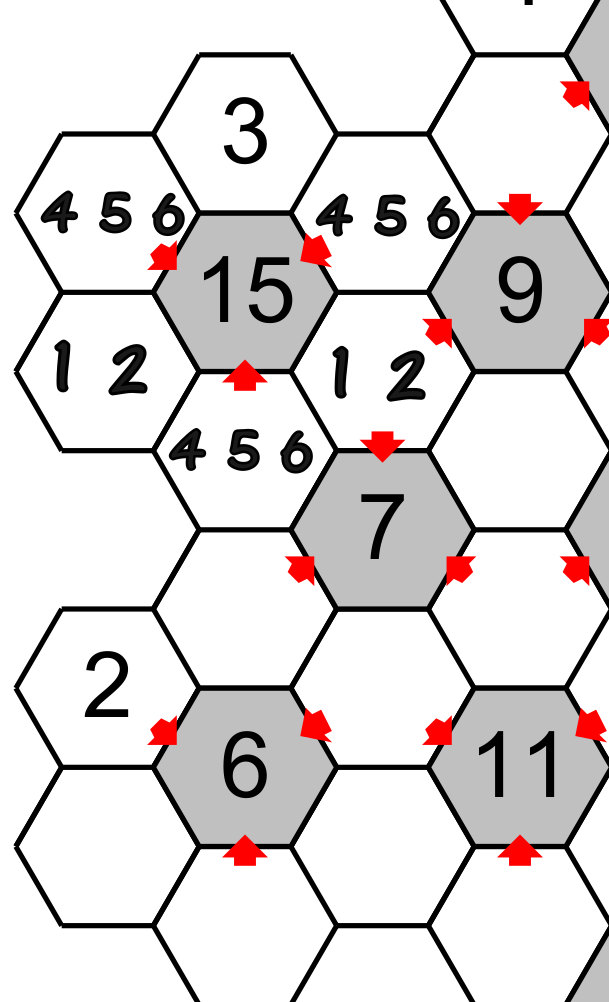
Suppose that later we figure out the number in a hexagon having a 2 (see the big red arrow), this hexagon point on a total of 7 which have a unique combination of numbers :1,2 and 4.
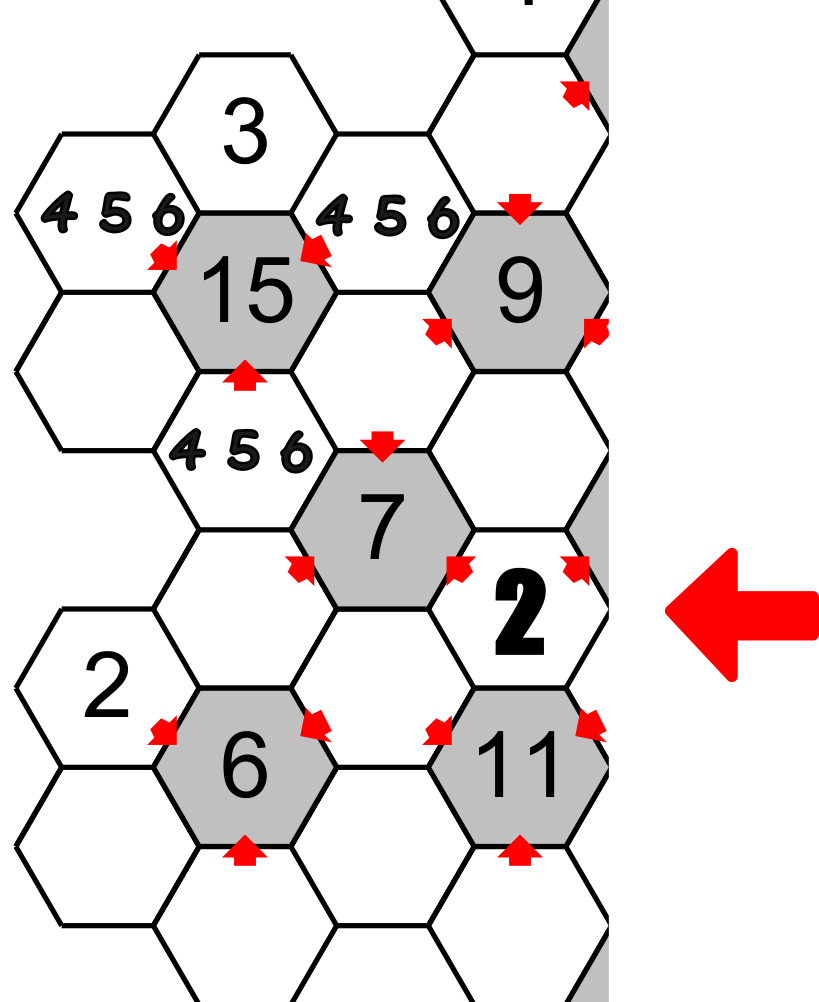
The hexagon situated between the total 15, 9 and 7, which we have already found 1 and 2 are possible candidates, cannot accept the 2 because this number is found around the 7. Then this hexagon will have the 1 and the other hexagon around the 15 will have 2 and finally the hexagon under the 7 will have 4. Notice that we could eliminate the candidate 4 under the 15.
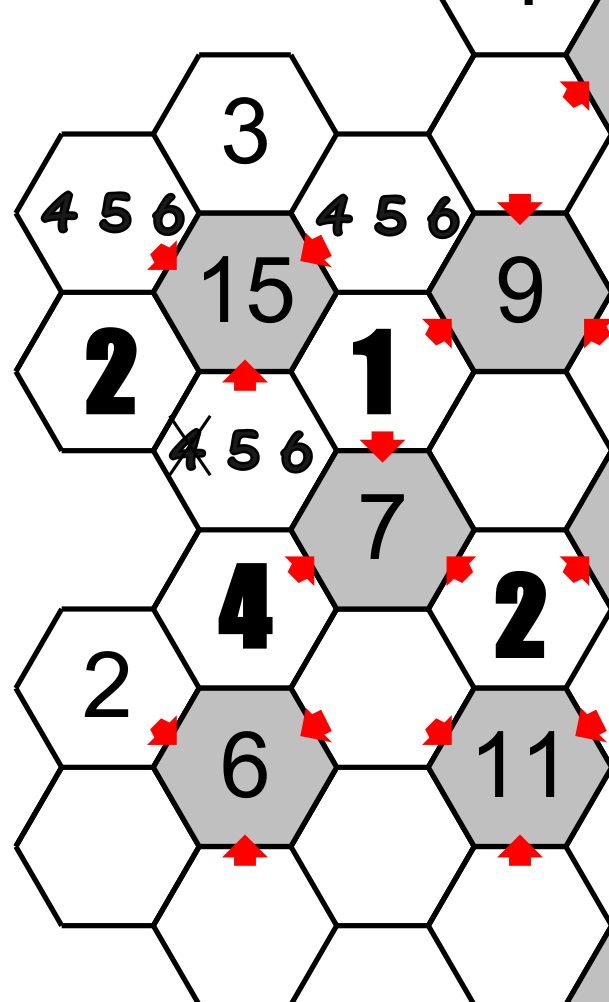
This is just an example of how to solve this game. In trying this puzzle you will discover other tricks, don't forget to bring an eraser.
This is a table showing the different combinations by total.
A puzzle and the solution.

















Comments powered by CComment