- Details
 GOAL
GOAL
This technic let you determine the right candidate.
 CONDITION
CONDITION
If a cell has n candidates and n neighboring cells pertaining to an another and same region and the neigboring cells have the same candidates than the original cell plus an another candidate. (It is very important that this other candidate appears only once in the neighboring cells).
 RESULT
RESULT
Then this other candidate must be elected in one of the neighboring cell else if this candidate does not appears it would produce an illegal sitation because the original cell will have no valid candidates (in fact the original cell will have 0 candidate).
Example
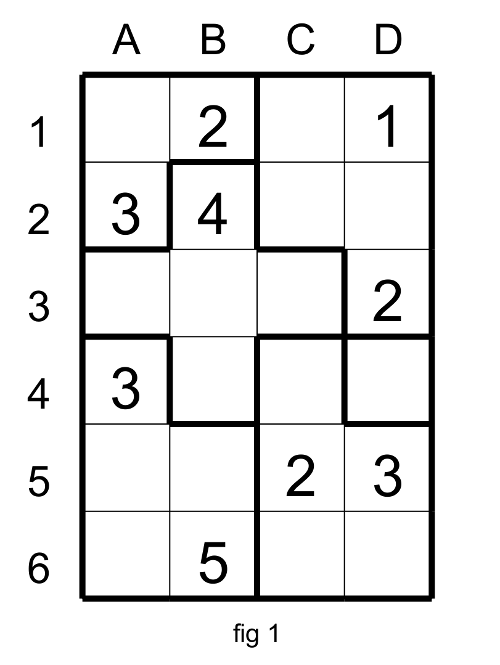
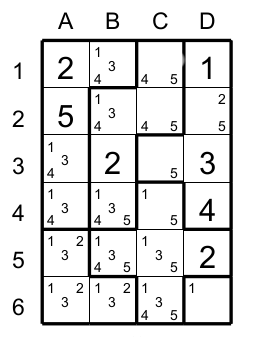
From the Suguru at the figure 1 with the basic technics we arrive at this situation (fig 2).
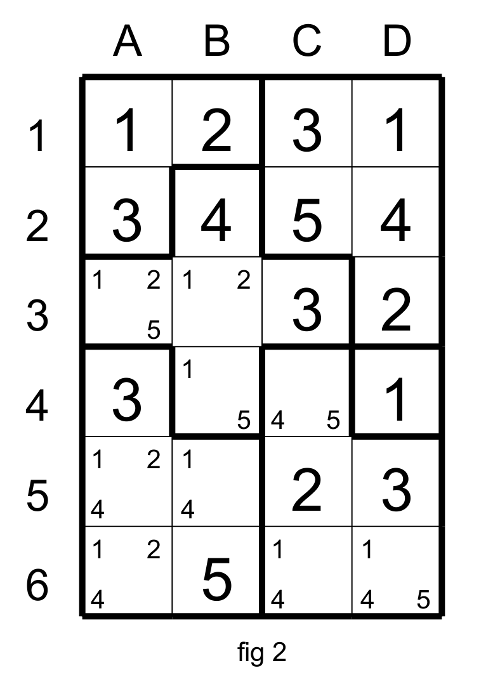
To be able to progress you need to apply the election. The original cell B5 has two candidates: 1 and 4 and also two neighboring cells C4 and C6. These two neighboring cells have together the same candidates that the original cell ( 1 and 4) plus an other candidate 5. So based on this rule C4 must have 5.
Why
If the candidate 5 were not present in C4 then C4 would have 4 and C6 1, thus the original cell B5 will have no candidate.
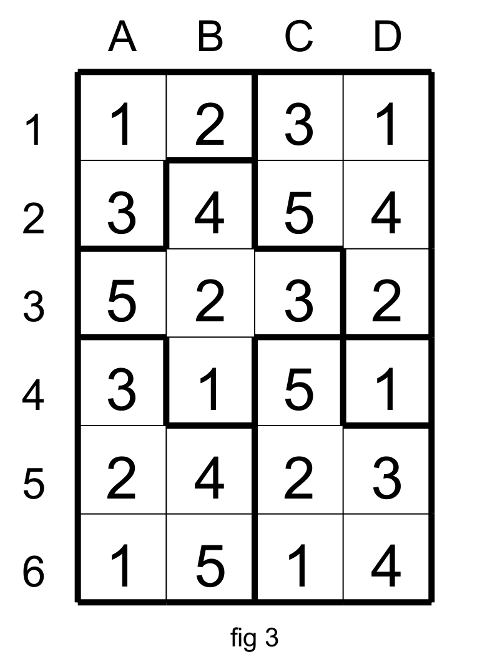
With that you could find the solution (fig 3).
You could try by yourself with this example Suguru election.pdf.
Write comment (0 Comments)- Details
Basic technics of resolution: the pair.
One of the most frequent and useful technic for solving Suguru is use of the pair. A pair is when two cells contain the same two candidates. To illustrate the concept, I use a Suguru that I have altered intentionaly the candidates in order to show you the effects of the pair. Obviously, by these alterations, I made the Suguru incoherent.
First of all we need to distinguish the location of the pair because you should be careful of this characteristic.
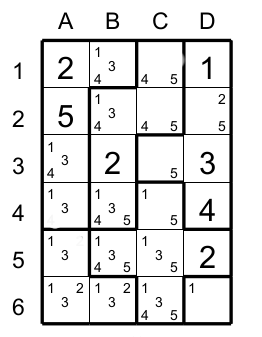
Look at the following figure 1.
Pair in the same region.
The region having the cells C1,C2,B2,B3 and B4 has a pair with the cell C1 and C2. Each one of these two cells has candidate 4 and 5. This means that these two numbers could only go in these two cell in this region. All the other cells in this same region, must not have the candidates 4 or 5. In this case we eliminate the candidate 4 in B2 and the candidates 4 and 5 in B4.
Pair in others regions.
If a cell from another region touchs the two cells from a pair in another region. Notice that the two cells having the pair must be in the same region. Then we could eliminate the candidates of the pair that are present in this cell. In this case the cell D2 touchs the pair C1 end C2. So the first condition is met : C1 and C2 are in the same region so we could eliminate 5 to D2. We could eliminate also the 4 to the cell B1 for the same reason.
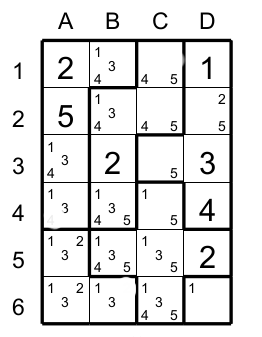
Now to illustrate an other case, suppose that cells A4 and A5 have only candidates 1 and 3 (figure 2).
Now the situation is if a cell (the original cell) touch a pair from two different regions, we could eliminate the candidates present in the pair from the original cell only if the two cells of the pair are neighborgs of each one. In the figue 2 the cell A4 and A5 have the two same candidates (1 and 3). Because these two cell are neighbourg, it means that in anay case they could have a 1 and a 3. And because the cell B5 touchs these two cells then we can eliminate 1 and 3 in B5. This is very important that the two cells of the pair are neighbourgs.
If the cells pertaining to the pairs are not neighbourg like in the figure 3.
Now suppose that the cell B6 has the candidates 1 and 3 instead of A5. The cell B5 touchs two cells having a pair, A4 and B6) from two different regions, because A4 and B6 are not neighbourgs then it means that the two cells could have the same number either 1 and 1 or 3 and 3 or 1 and 3. So we are not sure of the final result and we are not able to affect B5. Except if we are able to link these two cell by a chain. this latest technics is explained in the advance technics.
These technics could be generalized to trio (three cells having the same candidates) with the necessary adjustments.
Write comment (0 Comments)
- Details
RESOLUTION
In order to show you all the subtlety of this puzzle I solve for you a puzzle, I have added letters to designate each column and a number for each row for a better clarity.
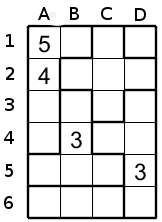
The first thing to consider is to look regions of size 1 (they are the easier to fill ), in this example the region at D1 occupy only one cell then this cell must have a 1. Look at the region in the upper left corner, this region is of size 5, then the numbers 1 to 5 must be included in this region. This region has already a 4 and 5, so it miss 1,2,3. The 3 could only go in B1 because the cell A3 and A4 touch the cell B4 with 3, then only B1 could accept the number 3.
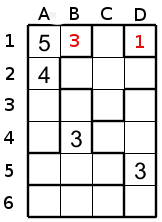
To help us it could be useful to write down in a cell the possible candidates, so in this region the cells A3 and A4 have the candidates 1 and 2.

The region of size 5 containing the number 3 in B4 illustrates an important method of resolution. The cell B3 cannot have a 4 (because A2 has 4) so this cell could only accept 1, 2 or 5. But we could also eliminate 1 and 2 because the cells A3 and A4 have only these two candidates, we only know that these two cells must have one of these numbers (in any order). In any case, these two cells touch the cell B3 therefore B3 cannot have 1 and 2 then only 5 remains for B3. Then the cells A5, B5 and C5 have candidates 1,2 and 4 (figure 4). Now each cell of the region of size 3 at A6,B6 and C6 has candidates 1,2 and 3. So if the cell B6 has a 1 or a 2 then any cells belonging to the other region (A5,B5 and C5) could not accept an 1 or a 2 because all these three cells touch B6 so it will be impossible to end the puzzle. Then B6 must have the only number that don't prevent us to complete the puzzle (because of the impossibility to put number), so B6 has 3
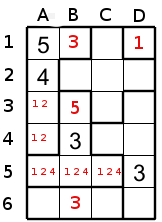
So by the same thinking B5 has 4 , because if the 4 is in A5 or in C5 the two remaining cells of this region containing candidates 1 and 2 will prevent us to fill either A6 or C6.
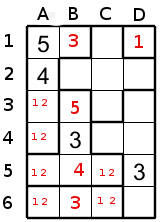
If we look at the up right region (the cross), we notice that 3 can only be in cell D2. Because all the other cells in this region touch a cell containing a 3.
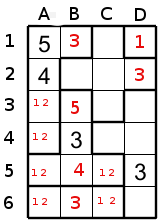
The number 5 goes to C1 for the same reason.
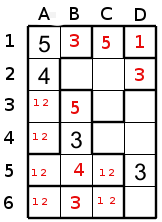
Now it seems that we reach a dead end. But look at the region of size 5 at the right ( with the cell D6). The cell D6 is a neighbour of C5 and C6 that could only accept 1 and 2, this means that the 1 and 2 will never be in D6 so these two candidates could only be in C4,D4 or D3 (with another candidate but we don't need to know the third candidate). Look at figure 8.
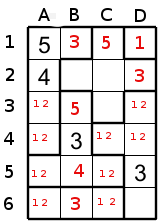
This means that the cell C3 could never have a 1 or a 2, and because C2 cannot have 1 then 1 goes in B2 and 2 goes in C2.
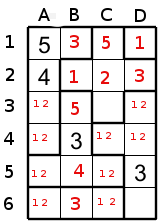
Now we could put 4 in C3 and we are able to resolve the puzzle to obtain the solution.
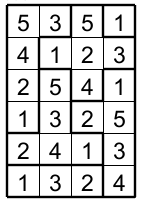
So that's all. This puzzle could give you enough challenges for your enjoyment.
Write comment (2 Comments)
- Details
A large part of my readers are from USA. I want to wish them an happy celbration for this fourth of July. !!!!

Happy Independence Day to all my american readers (and for the others also). !!!
Write comment (0 Comments)- Details

I am proud to tell you that this website is growing up, and it is celebrating his second birthday. Since last year I have added 128 articles in English and French. I have presented you some new puzzles like: Sudoku three Dimensions (9x9 and 16X16), the Balances and the old ones like Thermometer, Dot to Dot, Suguru, etc..
The popularity if this website has increased and I hope that it will continue. At first when I started this website I wanted to show you all my puzzles. But my other occupations have also increased, so I have a lot of other puzzles that are still unknown.
But the worst is that I am missing time to develop new ones or to improve old ones.
Now in my spare time I try to develop new functionalities to create more difficult Suguru, then I will need to upgrade also my rules’ page about Suguru to add the new resolution techniques.
But the most important thing I want to tell you: is that I enjoy your commerce ( social exchange) and I am more than happy to see your emails and comments.
To conclude, thank again.
Write comment (0 Comments)
















