 GOAL
GOAL
This technic let you eliminate one candidate.
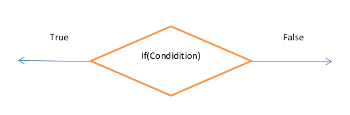 CONDITION
CONDITION
If a cell has n candidates and n neighboring cells pertaining to an another and same region (the region) and the neigboring cells have the same candidates than the original cell plus an another candidate. This another candidat must also appear only once in an aother cell (the another cell) of the region.
 RESULT
RESULT
Then we can exclude this other candidate in this other cell. Because the extra candidate must appear in the neighboring cells else it will create an illegal situation.
 WHY
WHY
The extra candidate must appear in the neighboring cells else it will create an illegal situation because the original cell with n candidats will have n neighbourgs with the same candidats.
EXAMPLE
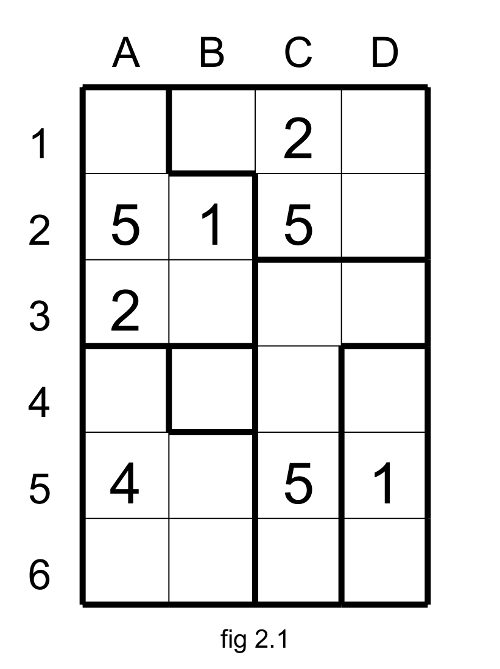
From the Suguru at the figure 2.1 with the basic technics we arrive at this situation (fig 2.2).
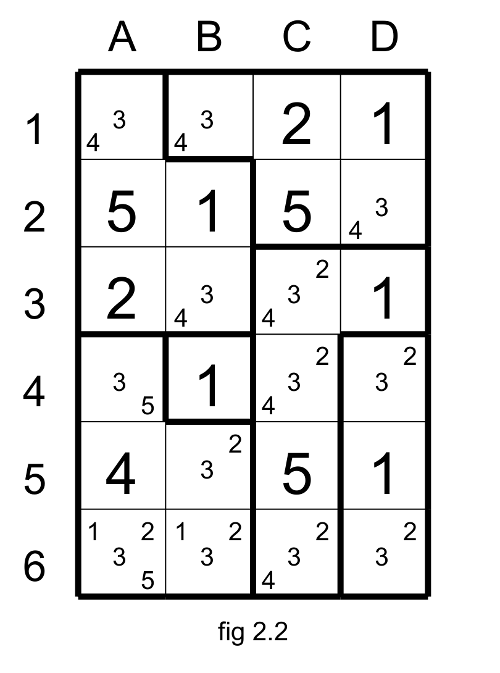
To be able to progress you need to apply the exclusion. The original cell B3 has two candidates: 3 and 4 and also two neighboring cells C3 and C4. These two neighboring cells have together the same candidates than the original cell ( 3 and 4) plus the candidate 2 twice (this is the difference with the technic of the Election, where the extra candidates must be unique in the neighboring cells). And this candidate 2 appears only once in this region (other than the neighboring cells) in C6. So we could eliminate the candidate 2 in C6.
Why
If the cell C6 has 2 then C3 and C4 will have candidates 3 and 4. It will result that B3 will be empty. Note we could also apply this technic with the original cell B5 and its neighboring cells C4 and C6 to eliminate the 4 in C3.
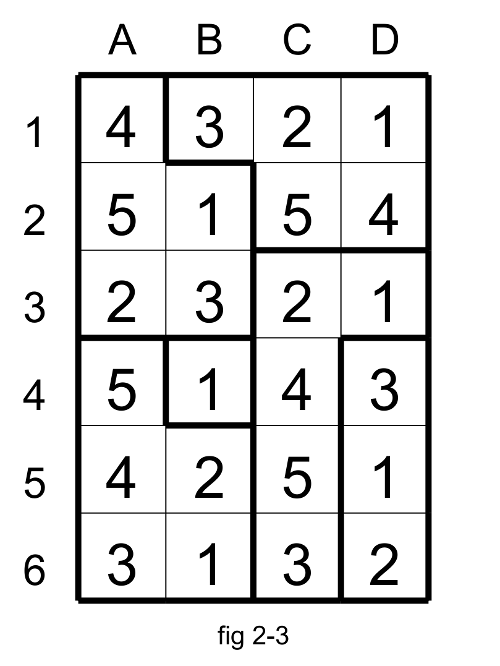
With that you could find the solution (fig 2.3).
You could try by yourself with this puzzle Suguru exclusion.pdf.

















Comments powered by CComment