YAKAZU
RULES OF YAKAZU
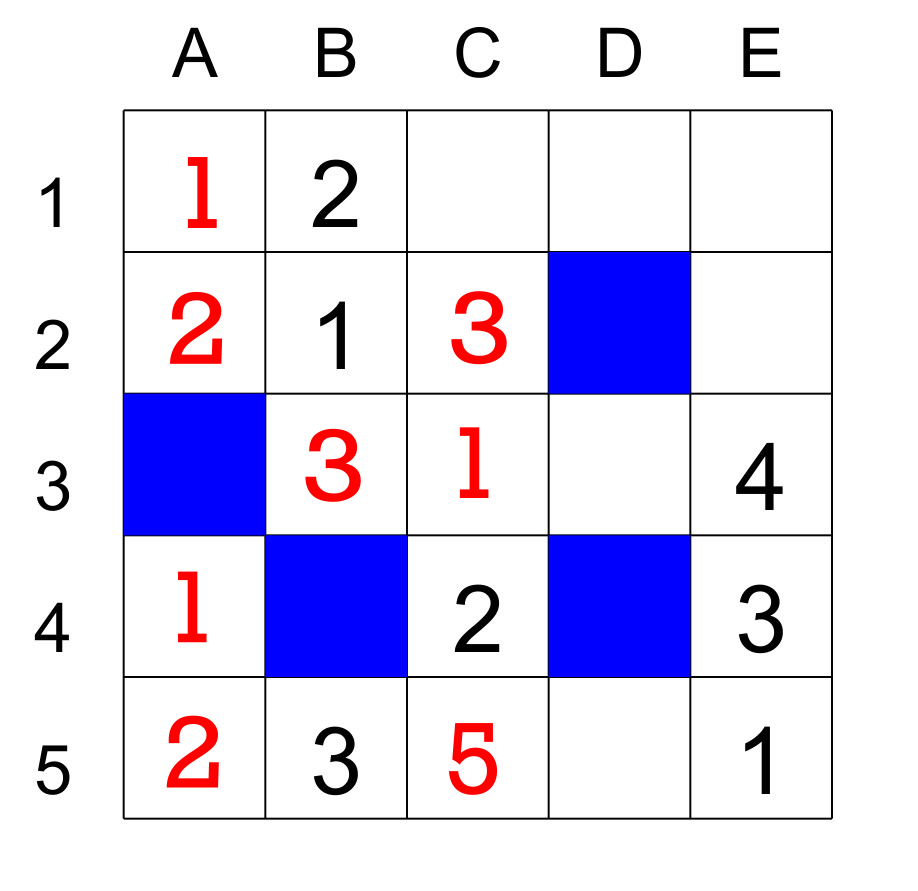
Yakazu is a cross between Sudoku and crossword. First of all, like the crossword puzzle, the grid contains black cells and like Sudoku, you have to enter numbers in the cells. The grid contains horizontal and vertical segments. A segment is a sequence of consecutive white cells. A segment larger than 1 must contain numbers from 1 to N (N being the length of the segment). At the beginning, some cells are filled. Here is a grid with its solution.

Each cell is part of two segments: horizontal and vertical. To make it easier to explain the rules, I will use coordinates and identify the rows by numbers and the columns by letters. Here is the grid with the coordinates.

Since we place numbers in a segment according to its size, the horizontal segment in row 1, which contains 5 cells, will contain the numbers 1 through 5. The vertical segment in A1 and A2 has a size of 2, so it will have the numbers 1 and 2. Since the cell A1 is common to both segments, this cell can never accept a number larger than the smallest segment it belongs to, in this case 2. There is an exception, if a segment has a size of 1 (like cells E2, A4 and D5) the rule does not apply, you have to take the size of the other segment of the cell as a bound. For example, E2, which is also part of the vertical segment of size 5 in column 5, will be able to accept only the numbers 2 and 5 as this last segment already contains 1, 3 and 4.
RESOLUTION
Here's how to solve this game. To start the grid, it is wise at the beginning to locate the shortest segments. The vertical segment A1 and A2, of size 2, can only contain the numbers 1 and 2. Since A1 crosses a horizontal segment that already has a 2 in cell B1 then A1 can only have 1, and therefore A2 must have 2.

We can complete the cells C2 and B3 which are each member of a segment of size 3. Since these two segments already have the numbers 1 and 2 then C2 and B3 will have 3.

Another useful method is to look for intersections of large segments. This is because those cells that are at the intersection of large segments are more likely to contain large numbers. In the grid, there are 4 segments of size 5: the two horizontal segments in rows 1 and 5 and the two vertical segments in columns C and E. For the segment in row 1 the maximum number in the segment, which is 5, can only be placed at the intersection of another segment of size 5, or at the intersection of a segment of size 1 (remember that the segment of size 1 can contain all the numbers in the other cross-segment). Since there are three possible intersections C1, D1 and E1, we cannot determine, at this point, where the 5 in the segment in row 1 will go. The same thing for the segment in column C, there are two possible intersections (C4 being busy) C1 and C5, so here again there is indecision. The vertical segment of column E has intercepts at E1 and E2 (segment size 1, which can accept a 5) so again indecision. The last segment of size 5, that of row 5, has two intersections with segments of the same size, C5 and E5, as E5 is already occupied, so only C5 can accept the 5.

The cell C3 cannot accept 2, 3, 4 or 5 so only the 1 will fit. Then we can place the 2 in cell A5 because this cell is at the crossroads of segments of size 2 and 5 and as there is already a 1 in the segment of 5 (square E1) then A5 will have 2 and by the same token A4 will have 1.
Afterwards, we can easily arrive at the solution.

These techniques will help you solve the easy and medium puzzles. For the more difficult ones, you need to use techniques that take into account the candidates. Candidates are all possible numbers that can fit in a square. These techniques are familiar to Sudoku or Suguru fans. To use these techniques, you must first determine the candidates for each cell. Here are some examples of techniques used to solve the most complicated Yakazu. Note that all the candidates are shown.
SINGLE PAIR
Principle.
If there are two cells in a segment which have the same two candidates then we can eliminate these two candidates in the other cells of the same segment. Because the other cells will not contain these candidates.
Example.

For example, in this grid, after identifying the candidates, we notice that the segment in row 3 has two cells A3 and C3, which have exactly the same candidates, i.e. 1 and 3. We can therefore eliminate candidates 1 and 3 in cells B3, D3 and E3. As a result, box E3 will contain the 2.
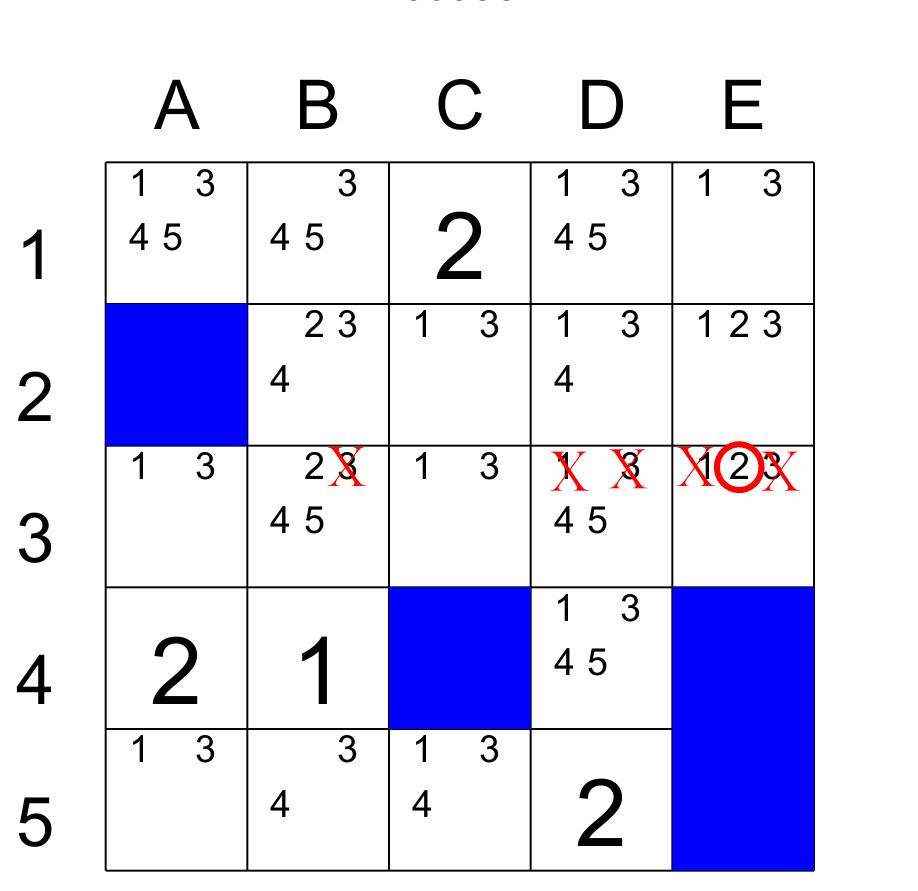
This can also apply to triplets. That is, three candidates in three boxes.
HIDDEN PAIR.
Principle.
A hidden pair exists when two cells of a segment have two candidates which are not in any other cell of the segment and these two cells have other candidates too. Then we can eliminate in these two cells the candidates which are not part of the pair.
Example.

In the segment in column D, the cells D1 and D3 have candidates 4 and 5 that are not found in any other cells in the segment. This means that these two cells will have these two candidates. We can therefore eliminate all candidates other than 4 and 5 in D1 and D3.
It will result that in the segment of row 1, the number 1 can only go to E1

XWING
Principle.
This method uses two different segments. It requires three conditions to apply.
- One segment has a candidate that can only go to two different cells.
- Another segment parallel to the first has the same candidate that can only go to two cells.
- The cells of the candidate of the first segment are perpendicular to the two squares of the second segment.
Then we can eliminate this candidate in all the other perpendicular cells of the two segments.
Example.

The segment in row 3 has candidate 4 who can only go to B3 and E3 (condition 1, a candidate who can only go to two cells). The segment of row 4 also has candidate 4 who can only go to B4 and E4 (condition 2, in a parallel segment, the same candidate, 4, can only go to two cells). And finally, the boxes B3 and B4 are perpendicular as well as E3 and E4 (condition 3).
This means that there will be either a 4 in B3 and E4 or a 4 in B4 and E3. In both cases we can eliminate the candidate 4 in columns B and E except for rows 3 and 4.

We will remove the candidate 4 in the boxes B1, E1 and E2. In B1 and E1 there will remain a single pair (with 3 and 5) and we can eliminate the 3 in A1 who will have 1. And the candidate 4 can only go to D1.
CONCLUSION
The most difficult games can include several of these techniques.
Like Suguru, Yakazu grids can take different sizes. Even if the size of the grid is bigger, the maximum size of the segments will always be 9. The different sizes of grids I produce range from 5x5 to 15x15.
If you want to trys the puzzles from this tuto (ZIP). yakazu.zip

















Comments powered by CComment