Arrows Maze

aa
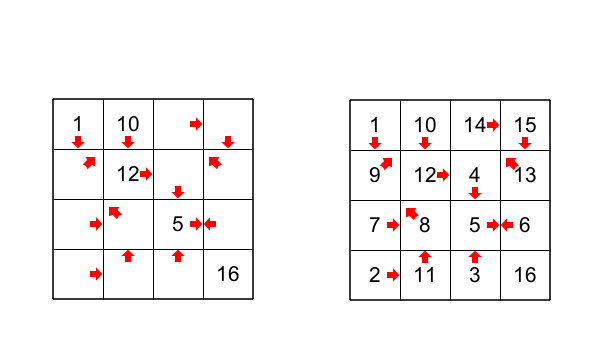
Figure 1
Arrows Maze
The goal is simple, you just have to reconstruct a path that goes through all the squares of a grid from the cell with the number 1 to the last cell (the cell wihtout arrow). The arrow in a cell indicates the direction of the next cell in the path. There are some cells that already have numbers, so you have to find the path.
In figure 1 there is a grid with the solution. To show you the subtleties of this puzzle, I will solve the following puzzle.
Resolution
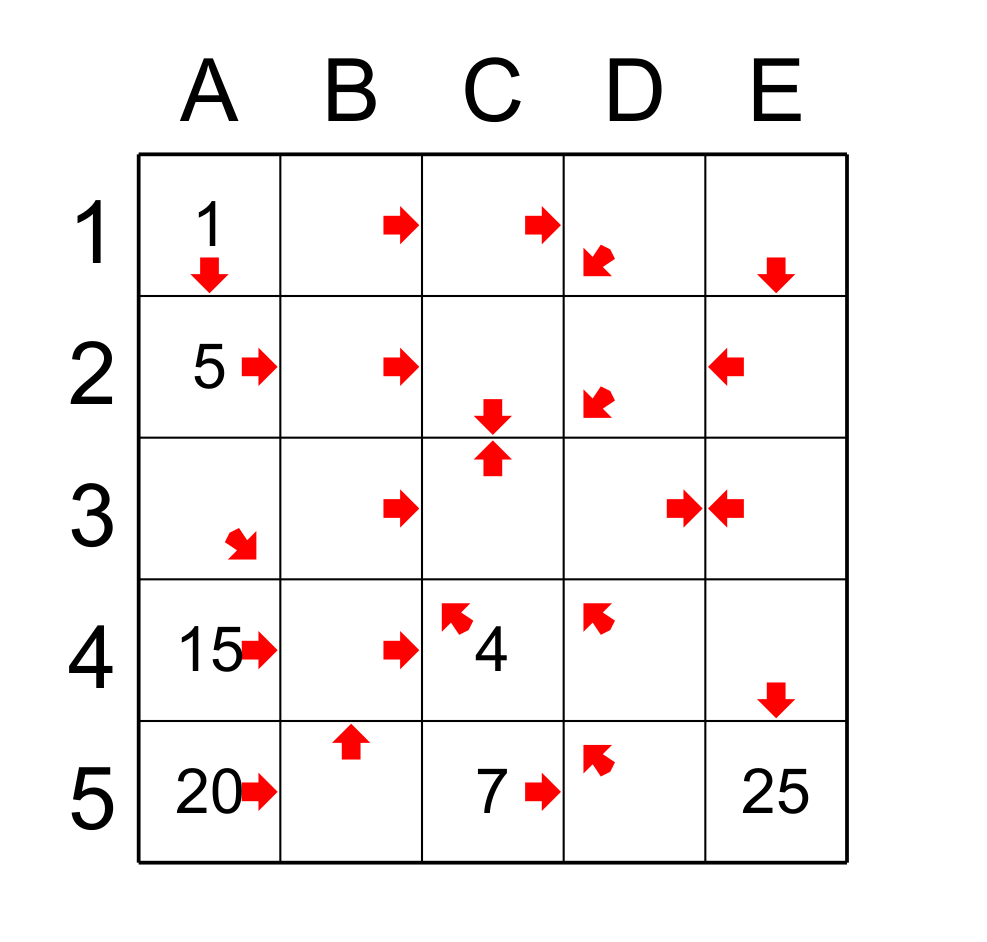
figure 2
For ease of explanation, I identify columns by letters and rows by numbers. So box A1 is at the intersection of column A and row 1. In order to clarify my explanations I will use the terms successor and predecessor, for example the predecessor of a cell before the number 10 is the cell that has the number 9 and the successor of cell 10 is the cell that has 11.
There are two main principles that will help you find the path.
1) If a cell points to only one possible cell, then that cell is the successor of the original cell.
2) If a cell is only pointed by one possible cell then that cell is the predecessor.
Here is the application of the successor principle. The cell A1 points to all the cells of the column A, but there is only one possible cell that can be the successor (i.e. to have the value 2) and it is the cell A3. So A3 gets the value 2. The cell A3 points to the cell B4 and C5 but only B4 can be the successor so B4 gets the value 3. We have the figure 3.
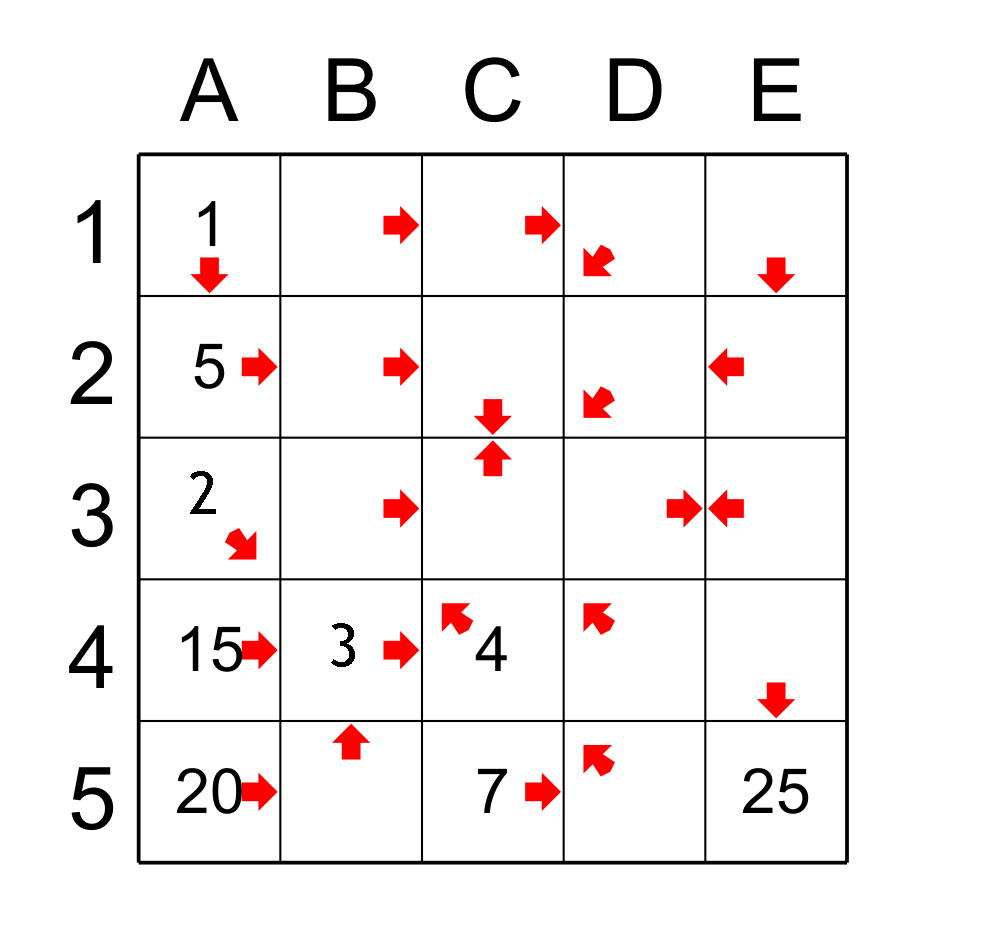
figure 3
Here is the application of the predecessor principle. The cell C5 which has the value 7 has three cells pointing to it: the cells A3 which has 2, A5 which has 20 and C2 which has no value yet. So the only cell that can be the predecessor of C7 is C2, which has the value 6. We can apply this reasoning to the cell A5 because there is only one cell that points to it, D2, so D2 will have the value 19. There is also only one cell that points to A4, it is the cell D1, so D1 is the predecessor of A4 and has the value 14.
The value of D5 is 8 because C5 is the only cell that points to it with the value 7. Once we know the value of D5 we find the value of B3 which has 9. Moreover B5 is the successor of the cell A5 so B5 has 21. Finally the cell C5 has only one square which points to it and it is C2 which obtains the value 6. Figure 4
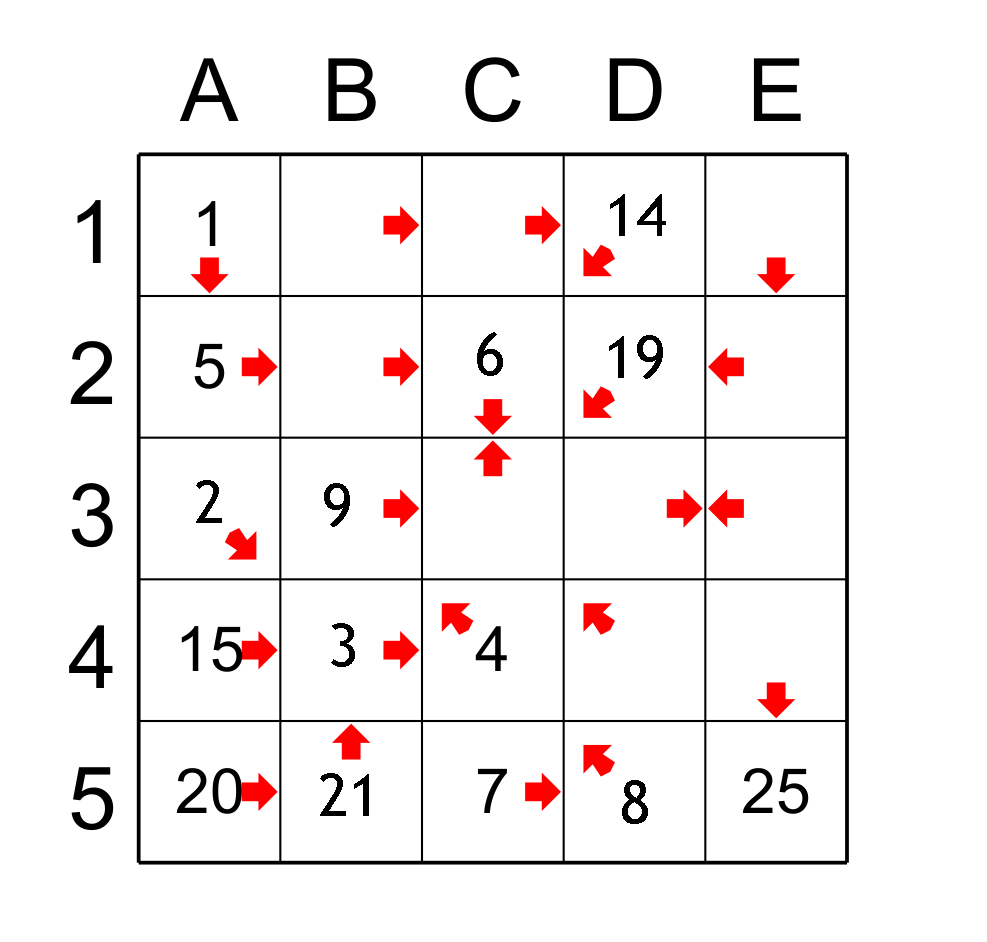
figure 4
We can still find cells with these principles: the cell E4 points only to E5 so it has the value 24. And as E4 is only pointed by the cell E1, then E1 is the predecessor with 23. We have reached the limits of these two principles and we must apply other reasoning. Figure 5.
.
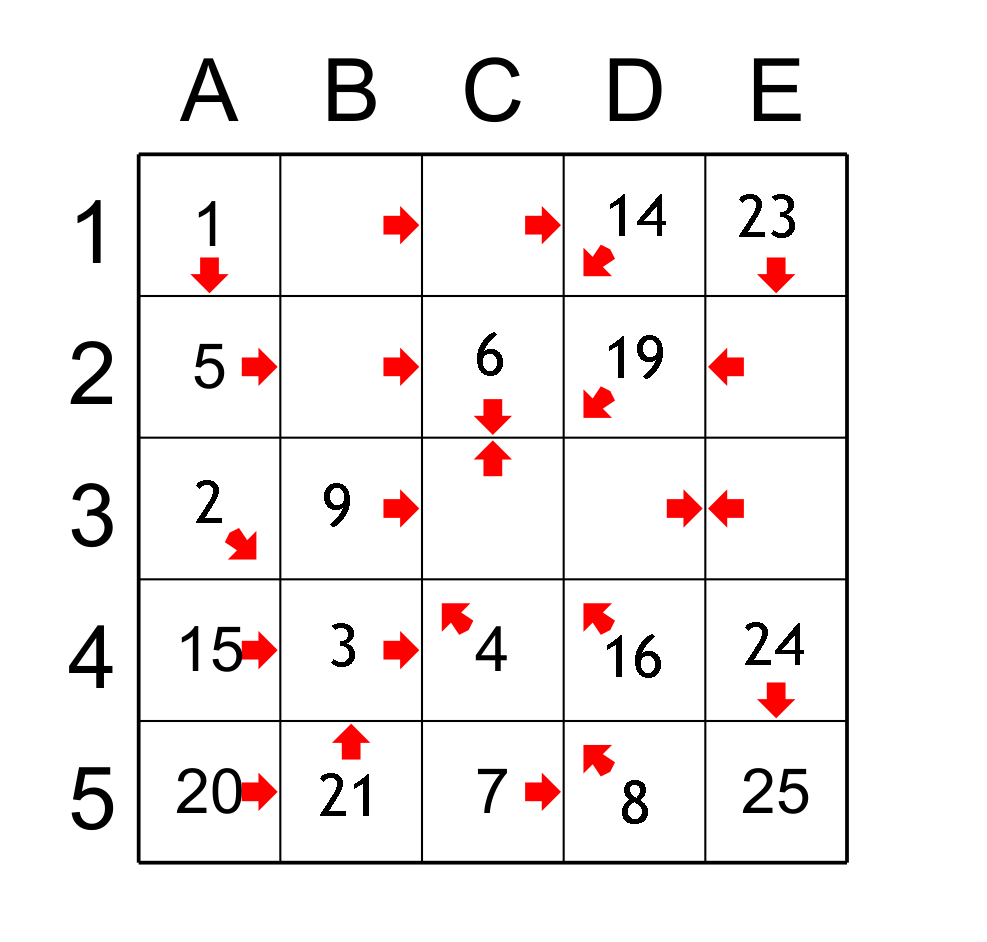
figure 4
In order to progress, we have to find the gaps. We have found the sequence from 1 to 9, from 14 to 16, from 19 to 21 and from 23 to 25. Now we have to find the gaps. It is often easier to deal with the smaller gaps between two sequences. So the gap between 21 (B5) and 23 (E1) is 1 because only one cell ( 22 ) is missing. So it is necessary to find a cell which will be the successor of the cell B5 and which will be at the same time the predecessor of the cell E1. Only the cell B1 fulfills this role so B1 gets the value 22.
The next smallest gap is between 16 (D4) and 19 (D3) which is two, so you have to find the cells that contain 17 and 18. The only cells that can obtain the values 17 and 18 are the cells B2 (which is the successor of D4) and the cell E2 which is the successor of B2 and at the same time the predecessor of D2. So B2 has 17 and E2 has 19 . Figure 5.
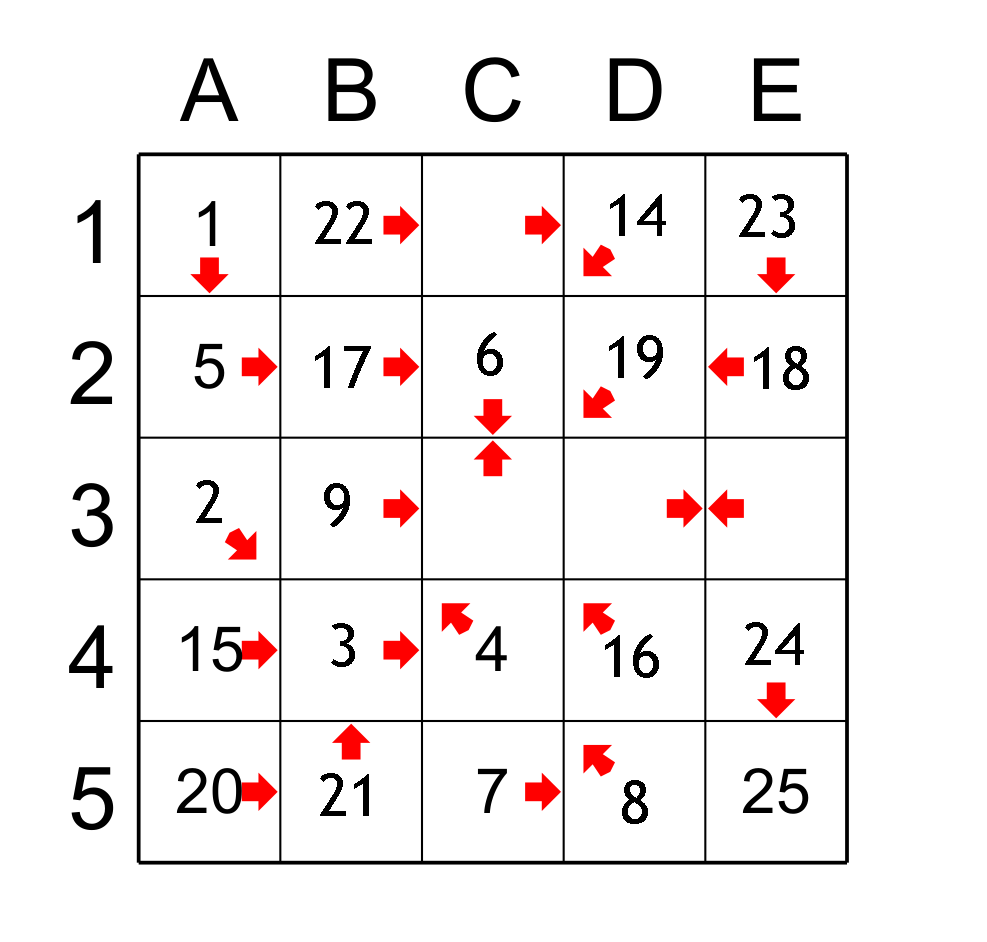
figure 5
Now there are four cells left and we must find the values between 9 and 14, i.e. 10, 11, 12 and 13. It is easier to determine the predecessor of D1 which is C1 (which obtains 13). Then, the predecessor of C1 is C3 which obtains the value 12 and the predecessor of C3 is E3 (which has 11) and the last square D3 has 10. Here the game is solved: figure 6.
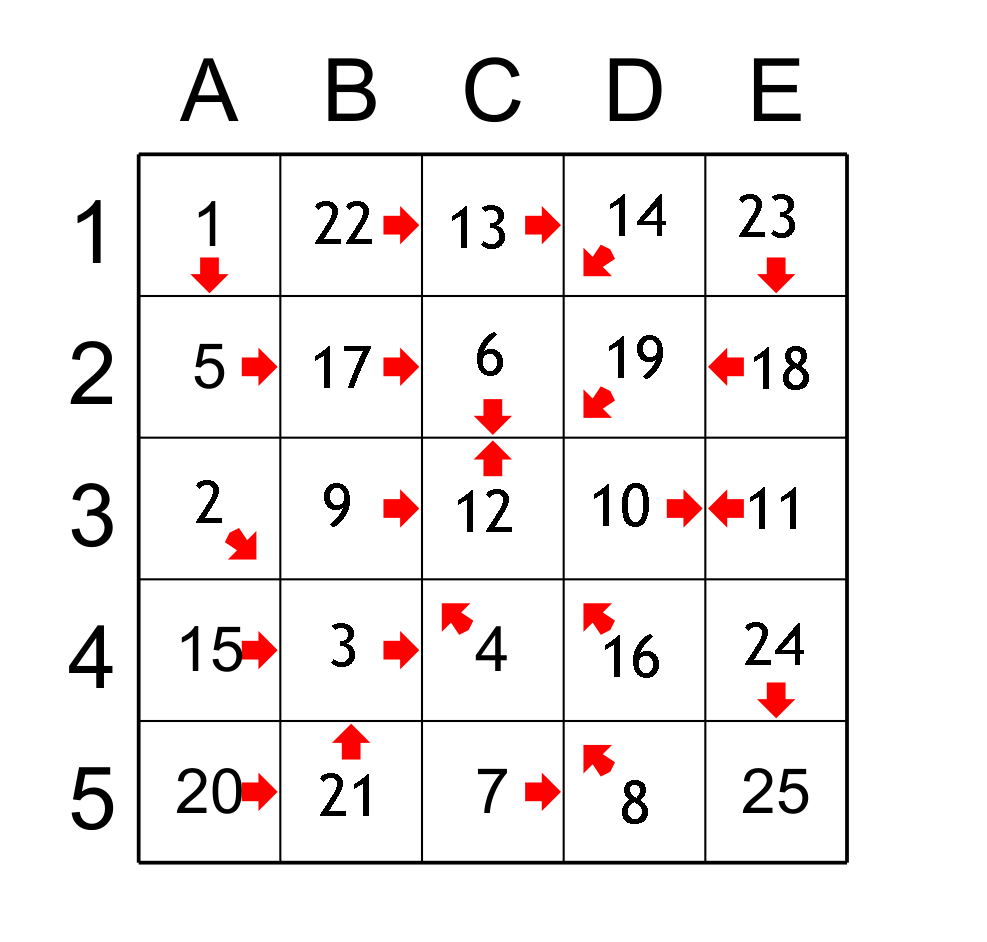
figure 6
You'll discover more solving techniques as you play... you'll love it.
{ccomment on}

















Terms & Conditions
Subscribe
Report
My comments