- Détails
Ripple Effect
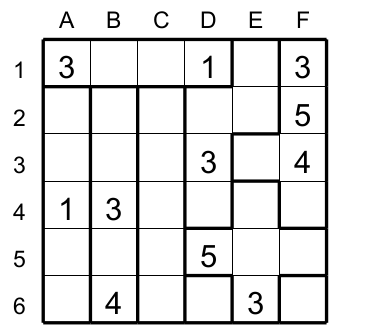
Le Ripple Effect (parfois nommé "Hakyuu", "Hakyuu Kouka", "Hakyukoka" ou "Sismic") est semblable au Suguru. Les règles pour les deux jeux sont similaires, entre autres une grille est subdivisée en région de tailles différentes (délimitées par les lignes foncées). Dans chaque région il faut entrer les nombres 1 à N (N étant la taille de la région). Les deux différences entre le Ripple Effect et le Suguru sont:
1) Un nombre N dans une case ne peut côtoyer le mème nombre dans les N cases qui sont situées à l'horizontael ou à la verticale de cette case.
2) Cela ne s'applique pas pour les cases situées en diagonale.
La figure 1 illustre ces règles. La case B4 (jaune) contient 3 donc les 3 prochaines cases (vert) qui sont situées à l'horizontale et à la verticale de B$ ne peuvent avoir de 3. Mais rien n'empêche les cases situées en diagonale de B4: A3,C3,A5 et C5 d'avoir 3.
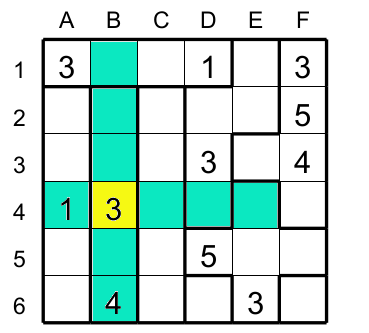
Figure 1
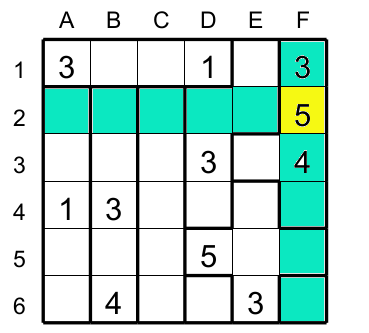
La figure 2 est un autre exemple; la case F2 qui a 5 ne peut tolérer d'avoir dans les cases vertes de 5.
J'ai identifié 5 types de techniques pour résoudre ce jeu.
Les deux premières sont familières à tout amateur de jeux (Sudoku, Suguru etc..)
1) Si une case a un seul candidat possible alors cette case doit contenir ce candidat.
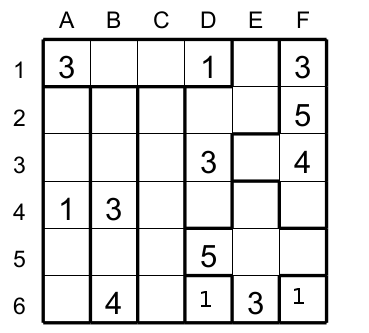
Dans la figure précédente les cases D6 et F6 sont les seules cases de ces deux régions de taille 1 donc d'après la définition une région de taille 1 ne peut avoir que 1. Comme 1 est le seul candidat alors D6 et F6 ont 1 (Figure 3).
2) Si une région a seulement un seul candidat alors la case ayant ce candidat doit avoir comme nombre ce candidat.
Par exemple (Figure 4), la case C2 est dans une région ayant les cases : B1,C2,C3,D3et D4. La case C2 a le candidat 4 qui n'est pas présent dans les autres cases de la région. Conclusion le 4 doit être en C2.
Maintenant voici une technique particulière au Ripple Effect.
3) Si dans une région il y a des candidats qui sont uniquement présents dans des cases qui sont situées sur une rangée ou colonne alors nous pouvons éliminer ces candidats dans les cases situées sur cette rangée ou colonne. Cela est dépendant du champ d'action du candidat (sa valeur).
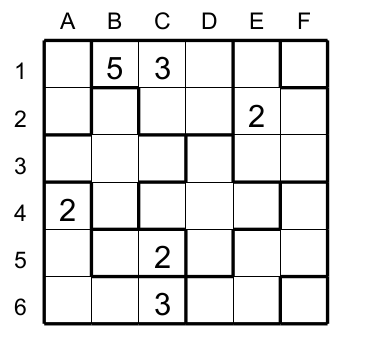
Concrètement, voici son application le jeu à la figure 5 après l'application des 2 premières techniques nous amène à la situation suivante (Figure 6).
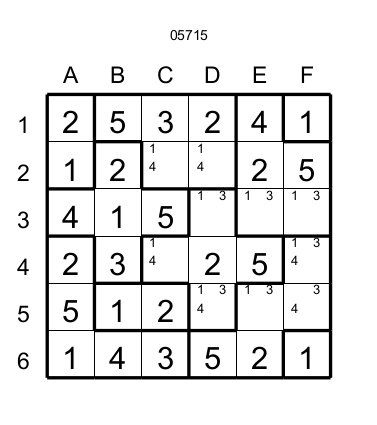
Les cases E3 et F3 sont dans la même région et elles sont situées sur une même rangé (la troisième) et de plus elles ont les candidats 1 et 3 qui ne sont pas présents ailleurs dans la région. Donc toutes les conditions sont là pour appliquer cette technique. Donc ces cases peuvent avoir soit 1 ou 3, si E3 a 1 alors on peut éliminer le 1 dans la case D3 qui est dans le champ d'action du candidat 1 dans E3, mais si F3 à 1 alors il n'y a aucun effet. Par contre, le 3 ayant un champ d'action plus grand (il faut au moins trois cases avant d'avoir un autre 3) s'il est placé dans la case F3 alors le 3 peut être éliminé en D3. Dans ce genre de situation il faut prendre le pire scénario est prendre la case la plus lointaine dans la rangée ou colonne pour appliquer cette technique.
4) Si une région a deux cases qui ont un canidat commun et que ce candidat ne se trouve pas dans d'autres cases de la région alors on peut éliminer ce candidat dans la case qui est sous le champ d'action des deux cases.
En résolvant le jeu suivant (figure 7) avec les trois premières techniques.
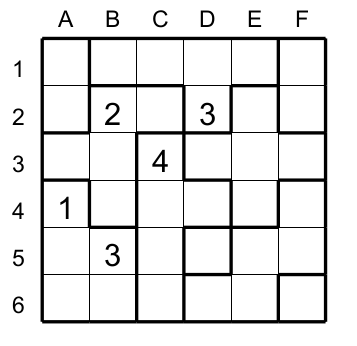
Cela donne la situation suivante (Figure 8)
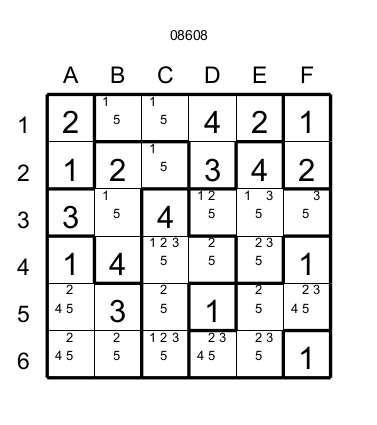Figure 8
Les cases D3 et E4 sont les deux seules cases de la région ayant comme candidat 2. Donc on peut éliminer le 2 dans la case D4 qui est sous l'influence de D3 et E4. Plus le candidat est élevé plus la case qui est sous le champ d'action pourra être loin.
Et la dernière technique.
5) Si une case contient un nombre et que de ce fait cela génère une situation invalide (par exemple, cela éliminerait un candidat dans toute une région) alors cette case ne peut contenir ce nombre et l'on peut éliminer ce candidat de cette case.
Après avoir appliqué les 4 premières techniques au jeu de la figure 9.
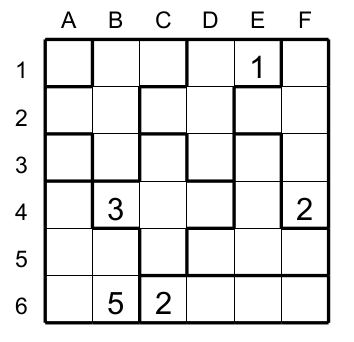
La situation de la figure 10 occure.
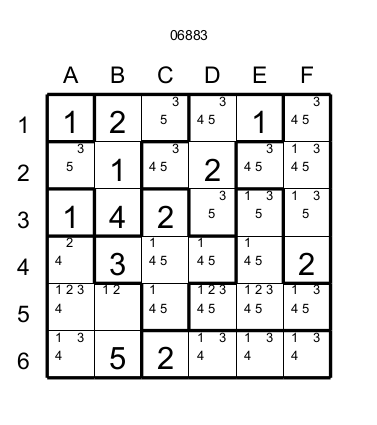Figure 10
La case C2 a les candidats 3,4 et 5. Si C2 a 3, cela éliminerait le candidat 3 dans les cases A2 et C1 et cette région n'aurait plus de candidat 3 donc nous pouvons éliminer le candidat 3 de C2. La même chose se produit pour le candidat 5 dans C2 car il produite une situation illégale (plus de 5 dans la région des cases A2 et C1, noue éliminons donc aussi le 5 en C2 et finalement c'est 4 qui émerge dans C2. Pour les jeux plus difficile parfois un chiffre dans une case peut provoquer par cascade (c.a.d une chaine forcée de coups) une situation illégale.
J'attribue à ces jeux une étoile en fonction de la technique (technique 1 = 1 étoile, technique 2 = 2 étoiles, etc..)
Ce jeu requiert parfois beaucoup de subtilités pour le résoudre. Si vous aimez les Suguru vous aimerez les "Ripple Effet". D'ailleurs si vous avez un nom francais à me proposer pour ce jeu, vous êtes les bienvenues. Pour l'instant je vais utiliser Ripple Effect.
Write comment (0 Comments)
