- Détails
Ce jeu est connu en anglais sous le nom de "Round Trip" ou "Grand Tour", comme il n'y avait pas de nom francais alors je le nomme Aller-Retour. Ce jeu a toute les qualités d'un bon puzzle: Il est simple et en même temps il peut être très captivant. Selon certaine source ce jeu aurait été inventé dans les années 1990, il est relativement inconnu.
Le but est de tracer un chemin passant par tous les points de manière à former un boucle. Chaque point est visité une seule fois. Les lignes reliants les points peuvent être horizontales ou verticales (jamais diagonales). À la fin le chemin doit toucher tous les points une fois seulement. Le chemin partant de n'inmporte quel point doit visiter tous les points et revenir a son point de départ. Au début certaint traits sont déssinés, il est à vous de compléter le tout.
Voici un exemple de jeu et de sa solution.
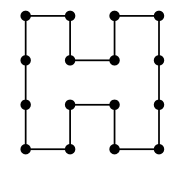
Pour y parvenir vous devez faire travailler vos neuronnes, rien n'est dû au hasard. Ce jeu peut avoir différentes tailles (de 4x4 à 18x18).
Quelques tuyaux.
Rien de mieux qu'un Aller-Retour réel (figure 1) pour illustrer ces techniques. Chaque colonne et rangée sont identifiée par des lettres ou chiffres pour vous aider à mieux suivre les explications.
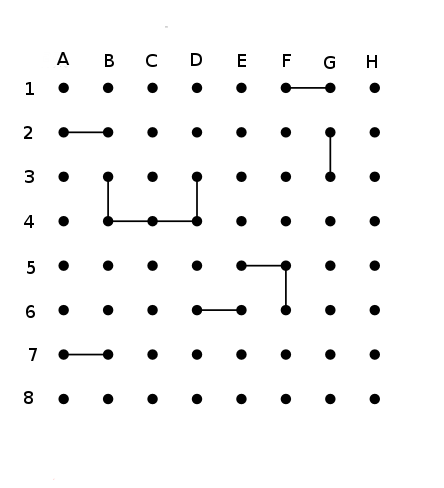
La toute première chose à retenir est que chaque point est visité une seule fois par le chemin, cela signifie que pour chaque point il ya une ligne entrante et un ligne sortante. On peut conclure que si un point à seulement deux directions possibles alors ces deux directions doivent avoir des lignes. Au début de chaque jeu les quatre points situé dans les quatre coins de la grille ont chacun deux directions possibles, nous pouvons donc tracer les deux lignes de chaque point. Cela nous fait donc à chaque fois 8 lignes gratuite !!! (voir figure 2)
Je vais vous montrer une situation à éviter a tout prix. Le point B1 a maintenant deux voies disponibles pour une seule ligne à tracer: soit vers C1 ou vers B2. Si la lligne est tracée vers B2 (figure 3), cela créé un circuit fermé entre les points A1,B1,A2 et B2. Donc il sera impossible de faire un boucle unique reliant tous les points.
Donc la ligne doit aller de B1 vers C1, car la direction vers B2 est éliminée (figure 4). Par le même raisonnement nous ajoutons une ligne de B8 vers C8.
.
Voici un autre truc pour vous aider dans certaines situations. Le point C3 a 3 directions possibles: C2,B3 et D3 ( le point C4 est éliminé car il a déja 2 lignes), pour deux lignes à tracer. Une possible configuation est d'avoir des lignes vers B3 et C3 (figure 5).
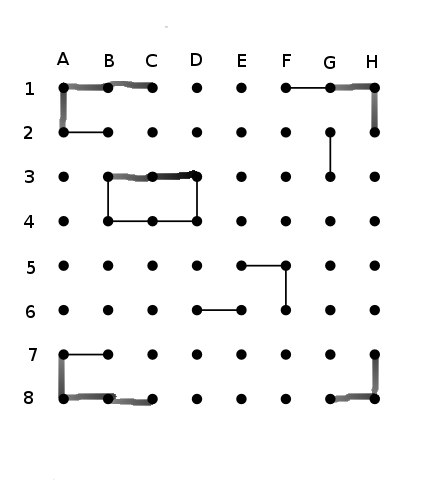Figure 5
Ces deux ligne forme une situation interdite (impossibilité d'avoir une boucll reliant tous les points) donc une ligne doit obligatoirement aller vers le point C2. Nous pouvons tracer cette ligne (figure 6) mêrme si nous ne savons pas où va l'autre ligne.
Ces ajoux de lignes ont créés des point ayant seulement deux voies possibles (A3 et A6) pour leurs deux lignes à tracer.Àpres avoir fait ces lignes, les deux points A4 et A5 ont chacun une seule voie de disponible et nous relions ces deux points ensemble (figure 7).
Vous avez maintenant assez de connaissances pour résoudre ce jeu. Vous devriez trouver la solution suivante (figure 8).
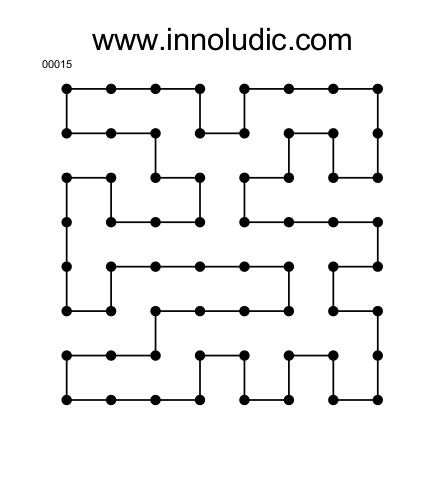
Si vous voulez le résoudre par vous même, télécharger le jeu ici. Pour conclure regardez toujours, après avoir tracer une ligne si cela créé une situation où des points ont le même nombre de ligne à tracer que de voie diponible. Si cela est le cas alors tracez les lignes. Plus vous faite d'Aller-Retour plus vous trouverez de technique de résolution.
Voilà, mainenant c'est à vous de jouer!.
J'attend vos commentaires si il y a lieu.
Write comment (0 Comments)
