RÉSOLUTION
Voici un exemple de résolution d'une grille, j'ai ajouté des lettres pour identifier les colonnes et des nombres pour les rangées.
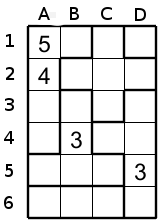
La première chose à considérer, c'est de remplir immédiatement les régions de taille 1. Ici il y a une seule région de taille 1 la case D1 donc nous inscrivons 1 a D1. Ensuite il faut voir si certains chiffres ne peuvent aller que seulement dans une seule case. Par exemple la région de taille 5 du haut a gauche contient déja 4 et 5 donc les trois autres cases de cette région doivent avoir 1,2 et 3. Mais les cases A3 et A4 touchent B4 qui contient un 3 alors le 3 ne peut qu'aller qu'en B1.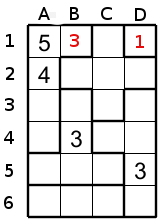
Pour nous aider nous inscrivons les candidats possibles dans les cases restantes. Donc A3 et A4 ont 1 et 2 comme candidats.

La région de taille 5 contenant le 3 en B4 illustre une méthode utile de résolution en effet la case B3 ne peut avoir de 4 (sa voisine A2 a un 4) de plus cette même case est voisine de A3 et A4 qui elles ne peuvent contenir que 1 et 2 et comme ces deux cases (soit A3 et A4) touchent toute deux B3 alors B3 ne peut accepeter de 1 et 2 alors le seul chiffre restant que peut accepter B3 est 5. Ce qui signifie que les cases A5,B4 et C5 ont comme candidats possible: 1,2 et 4. La région de taille 3 immédiatement en dessous (cases A6,B6 et C6) ne peut que contenir quant à elle que les nombres 1 à 3. Donc si la case B6 a soit 1 ou 2 alors il sera impossible de placer un de ces deux chiffres dans les cases A5,B5 et C5. Car B6 est voisine de ces trois cases. Donc B6 doit contenir 3 sinon le jeu est irréalisable.
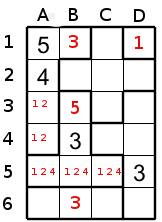
Par le même raisonnement B5 a 4 car si A4 a 4 ou C4 a 4 alors les deux autres cases auront 1 et 2 et alors une des deux cases libres (A6 et C6 de région de taille 3) ne pourront être emplies. Donc B5 doit contenir un 4.
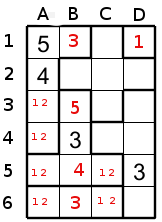
Dans la région du haut (en forme de croix) la seule case qui peut accepter le 3 est D2, car toutes les autres cases libres de cette région touchent à une case qui a un 3.
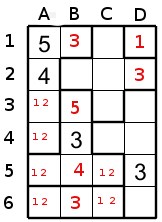
Nous pouvons ainsi placer le 5 à C1.
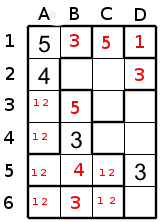
Pour progresser il nous faut réfléchir un peu. La case D6, dans une région de taille 6, est voisine des cases C5 et C6 qui elles ne peuvent que contenir 1 ou 2 alors D6 ne peut avoir ces deux nombres. Il seront alors nécessairement en C4 d4 ou D3 (plus un autre candidat bien sûr). voir la figure 8
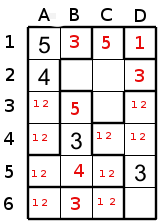
Ce qui signifie que C3 ne pourra avoir de 1 ou de 2 car elle est voisine des 3 cases possibles qui peuvent contenir ces nombres dans la région voisine. Donc le 1 et 2 doivent aller en B2 ou C2 mais comme C2 ne peut avoir de 1 alors B2 a le 1 et C2 a le 2.
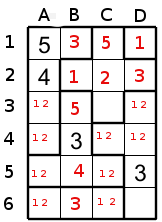
On place le 4 en C3 et le reste est un jeu d'enfant... nous obtenons la solution suivante.
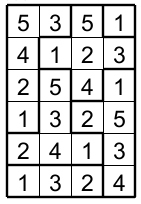
Ainsi vous pouvez résoudre des Suguru. C'est un jeu plein de défis.



















Comments powered by CComment