YAKAZU
LES RÈGLES du YAKAZU
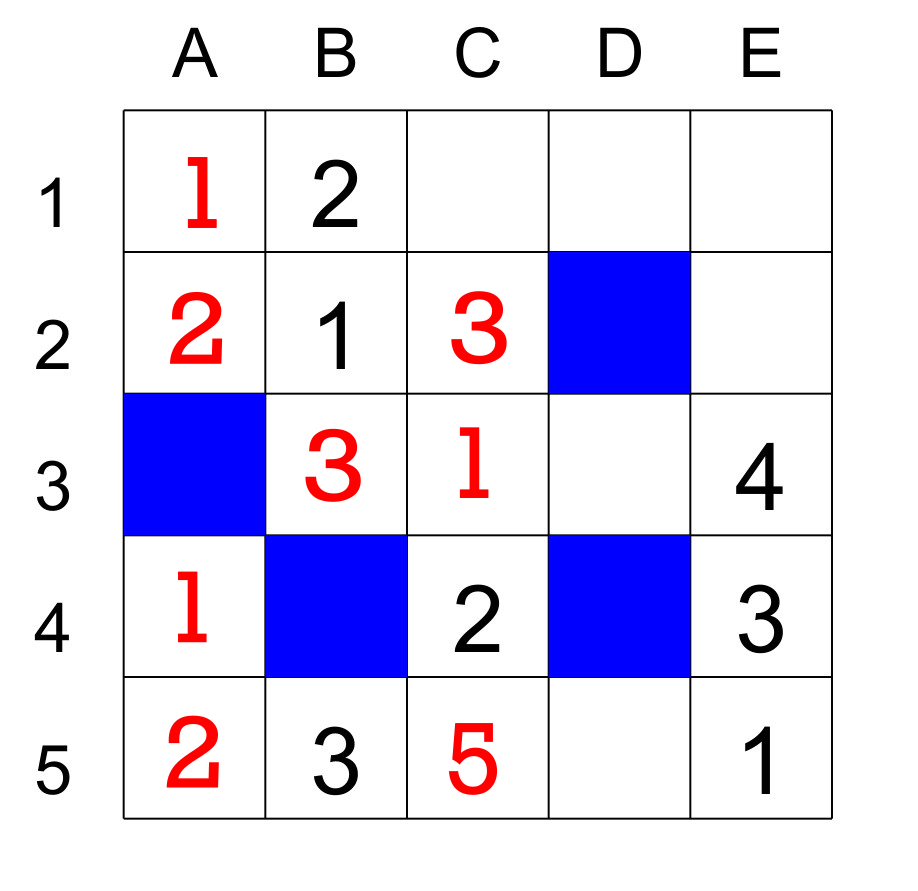
Le Yakazu est un croisement entre le Sudoku et les mots croisés. D’abord, comme les mots croisés, la grille contient des cases noires et comme au Sudoku, il faut entrer des nombres dans les cases. La grille contient des segments horizontaux et verticaux. Un segment est une suite de cases blanches consécutives. Un segment plus grand que 1 doit contenir les nombres de 1 jusqu’à N (N étant la longueur du segment). Au début, certaines cases sont remplies. Voici une grille avec sa solution.

Chaque case fait partie de deux segments : horizontal et vertical. Pour faciliter les explications des règles, je vais utiliser des coordonnées et identifier les rangées par des chiffres et les colonnes par des lettres. Voici la grille avec les coordonnées.

Comme on place les nombres dans un segment en fonction de sa taille, le segment horizontal de la rangée 1, qui contient 5 cases, contiendra les nombres de 1 à 5. Le segment vertical en A1 et A2 a une taille de 2, donc il aura les nombres 1 et 2. Comme la case A1 est commune à ces deux segments, cette case ne pourra jamais accepter de nombre plus grand que le plus petit segment à laquelle elle appartient, dans ce cas-ci : 2. Il y a une exception, si un segment a une taille de 1 (comme les cases E2, A4 et D5) la règle ne s’applique pas, il faut prendre la taille de l’autre segment de la case comme borne. Par exemple, E2, qui fait aussi partie du segment vertical de taille 5 sur la colonne 5, pourra accepter seulement les nombres 2 et 5 ce dernier segment contient déjà 1,3 et 4.
RÉSOLUTION
Voici comment résoudre ce jeu. Pour commencer la grille, il est avisé au début de repérer les segments les plus courts. Le segment vertical A1 et A2, de taille 2, ne peut contenir que les nombres 1 et 2. Comme A1 croise un segment horizontal qui a déjà un 2 dans la case B1 alors A1 ne peut qu’avoir 1, et par conséquent A2 doit avoir 2.

Nous pouvons compléter les cases C2 et B3 qui sont chacune membre de segment de taille 3. Comme ces deux segments ont déjà les nombres 1 et 2 alors C2 et B3 auront 3.

Une autre méthode utile est de rechercher les intersections de grands segments. Car ces cases qui sont à l’intersection de grands segments sont plus susceptibles de contenir de grands nombres. Dans la grille, il y a 4 segments de taille 5 soit les deux horizontaux des rangées 1 et 5 et les deux verticaux des colonnes C et E. Pour le segment de la rangée 1 le nombre maximal du segment, qui est 5, peut seulement être placé à l’intersection d’un autre segment de taille 5, ou à l’intersection d’un segment de taille 1 (rappelez-vous que le segment de taille 1 peut contenir tous les nombres de l’autre segment transversal). Comme il y a trois intersections possibles C1, D1 et E1, nous ne pouvons pas déterminer, pour le moment, où ira le 5 du segment de la rangée 1. La même chose pour le segment de la colonne C, il y a deux intersections possibles (C4 étant occupé) C1 et C5, alors ici aussi il y a indécision. Le segment vertical de la colonne E a des interceptions en E1 et en E2 (segment de taille 1, qui peut accepter un 5) donc indécision encore. Le dernier segment de taille 5, celui de la rangée 5, a deux intersections avec des segments de mêmes tailles soit C5 et E5 comme la case E5 est déjà occupée, alors seule C5 peut accueillir le 5.

La case C3 ne peut accepter ni 2, 3, 4 ou 5 alors seulement le 1 peut convenir. Ensuite, nous pouvons placer le 2 dans la case A5 car cette case est à la croisée de segments de taille 2 et 5 et comme il y a déjà un 1 dans le segment de 5 (la case E1) alors A5 aura 2 et par le fait même A4 aura 1.
Par la suite, nous pouvons aisément arriver à la solution.

Ces techniques vous aideront à résoudre les jeux facile et moyen. Pour les plus difficiles, il faut utiliser des techniques qui tiennent compte des candidats. Les candidats sont tous les nombres possibles qui peuvent aller dans une case. Ce sont des techniques sont familières aux adeptes de Sudoku ou de Suguru. Pour utiliser ces techniques, il faut, en premier lieu, déterminer les candidats de chaque case. Voici des exemples de techniques utilisées pour résoudre les Yakazu les plus compliqués. Notez que tous les candidats sont indiqués.
PAIRE SIMPLE
Principe.
S’il y a deux cases dans un segment qui ont les mêmes deux candidats alors on peut éliminer ces deux candidats dans les autres cases du même segment. Car les autres cases ne pourront contenir ces candidats.
Exemple.

Par exemple dans cette grille, après avoir identifié les candidats, nous remarquons que le segment de la rangée 3 a deux cases A3 et C3, qui ont exactement les mêmes candidats soit 1 et 3. Nous pouvons donc éliminer les candidats 1 et 3 dans les cases B3, D3 et E3. Il en résultera que la case E3 contiendra le 2.
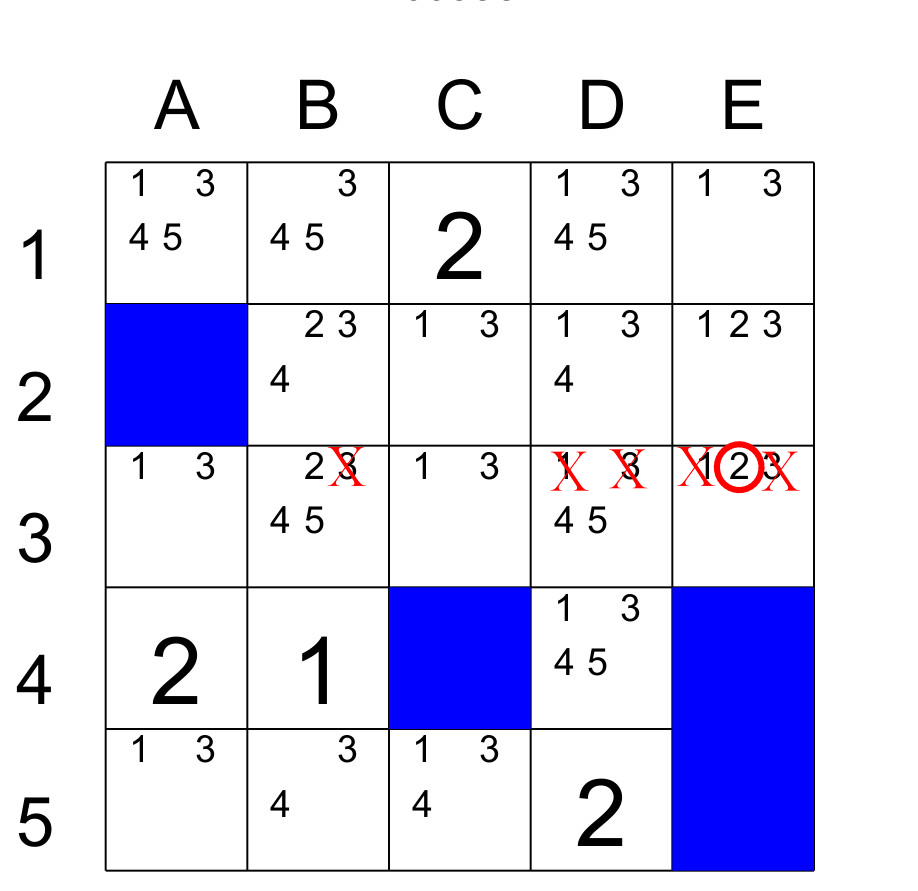
Cela peut s’appliquer aussi pour des triplets. C’est-à-dire trois candidats dans trois cases.
PAIRE CACHÉE.
Principe.
Une paire cachée existe lorsque deux cases d’un segment ont deux candidats qui ne se trouvent dans aucune autre case du segment et que ces deux cases ont d’autres candidats aussi. Alors on peut éliminer dans ces deux cases les candidats qui ne font pas partie de la paire.
Exemple.

Dans le segment de la colonne D, les cases D1 et D3 ont les candidats 4 et 5 qui ne se retrouvent pas dans aucune autre case du segment. Cela signifie que ces deux cases auront ces deux candidats. Nous pouvons donc éliminer tous les candidats autres que 4 et 5 dans D1 et D3.
Il en résultera que dans le segment de la rangée 1, le nombre 1 ne pourra aller qu’en E1.

XWING
Principe.
Cette méthode utilise deux segments différents. Il faut trois conditions pour qu’elle s’applique.
- Un segment a un candidat qui ne peut qu’aller que dans deux cases différentes.
- Un autre segment parallèle au premier a le même candidat qui ne peut qu’aller que dans deux cases seulement.
- Les cases du candidat du premier segment sont perpendiculaires aux deux cases du deuxième segment.
Alors on peut éliminer ce candidat dans toutes les autres cases perpendiculaires des deux segments.
Exemple.

Le segment de la rangée 3 a le candidat 4 qui ne peut qu’aller qu’en B3 et E3 (condition 1, un candidat qui ne peut qu’aller dans deux cases seulement). Le segment de la rangée 4 a également le candidat 4 qui ne peut qu’aller en B4 et E4 seulement (condition 2, dans un segment parallèle, le même candidat, 4, ne peut qu’aller qu’en deux cases). Et finalement, les cases B3 et B4 sont perpendiculaires ainsi que E3 et E4 (conditions 3).
Cela veut dire qu’il y aura soit un 4 en B3 et E4 ou soit un 4 en B4 et E3. Dans les deux cas on peut éliminer le candidat 4 dans les colonnes B et E sauf pour les rangées 3 et 4.

On enlèvera le candidat 4 dans les cases B1, E1 et E2. Il restera dans les cases B1 et E1 une paire simple (avec 3 et 5) et nous pourrons éliminer le 3 en A1 qui aura 1. Et le candidat 4 ne pourra qu’aller en D1.
CONCLUSION
Les jeux les plus difficiles peuvent comprendre plusieurs de ces techniques.
Tout comme le Suguru, les grilles de Yakazu peuvent prendre différentes dimensions. Même si la taille de la grille est plus grande, la taille maximum des segments sera toujours de 9. Les différentes tailles de grilles que je produis vont de 5x5 jusqu’à 15x15.
Si vous voulez essayer les grilles de ce tuto (ZIP). yakazu.zip



















Comments powered by CComment