Laby Flèches

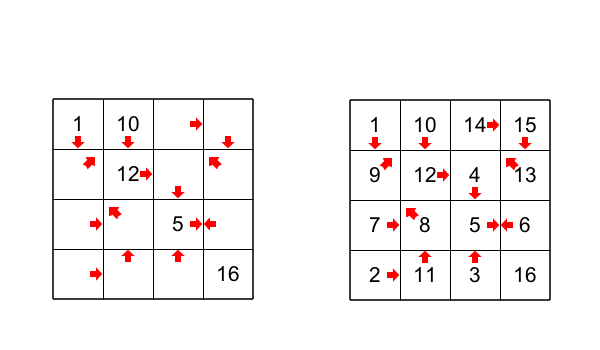
Figure 1
Le Laby Flèches
Ce jeu est connu sous le nom anglais de « Arrows Maze », comme je ne pas vue de traduction en français j’ai décidé de le nommer Laby Flèches.
Le but est simple, il suffit de reconstituer un chemin qui parcourt toutes les cases d'une grille à partir de la case ayant le 1 jusqu’à la dernière case (la case qui n’a pas de flèche). La flèche dans une case indique la direction où se trouve la case suivante du trajet. Il y a quelques cases qui ont déjà des nombres, à vous de trouver le chemin.
Dans la figure 1 il y a une grille avec la solution. Pour vous monter les subtilités de ce jeu, je vais résoudre le jeu suivant.
Résolution
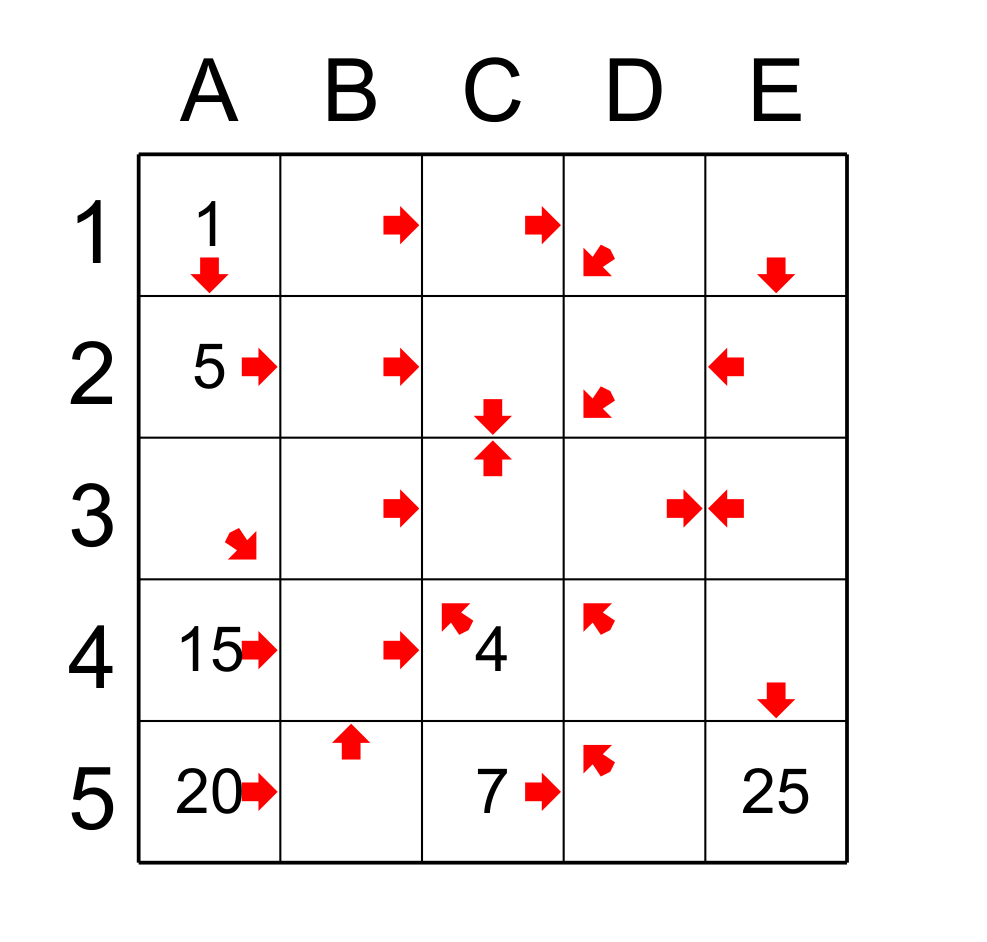
figure 2
Pour faciliter les explications, j’identifie les colonnes par des lettres et les rangées par des chiffres. Donc la case A1 est à l’intersection de la colonne A et de la rangée 1.
Dans le but de clarifier mes explications, je vais utiliser les termes successeur et prédécesseur. Par exemple le prédécesseur d’une case avant le nombre 10 est la case qui a le nombre 9 et le successeur de la case 10 est la case qui a 11.
Il y a deux grands principes qui vous aideront à trouver le chemin.
1) Si une case pointe vers une seule case possible alors cette case est le successeur de la case d’origine.
2) Si une case est seulement pointée par une case possible alors cette case est le prédécesseur.
Voici l’application du principe du successeur. La case A1 pointe sur toutes les cases de la colonne A, mais il y a seulement une case possible qui peut être le successeur c’est-à-dire d’avoir la valeur 2 et c’est la case A3. Donc A3 obtient la valeur 2. La case A3 pointe sur les cases B4 et C5 mais seulement B4 peut être le successeur donc B4 obtient la valeur 3. Nous avons la figure 3.
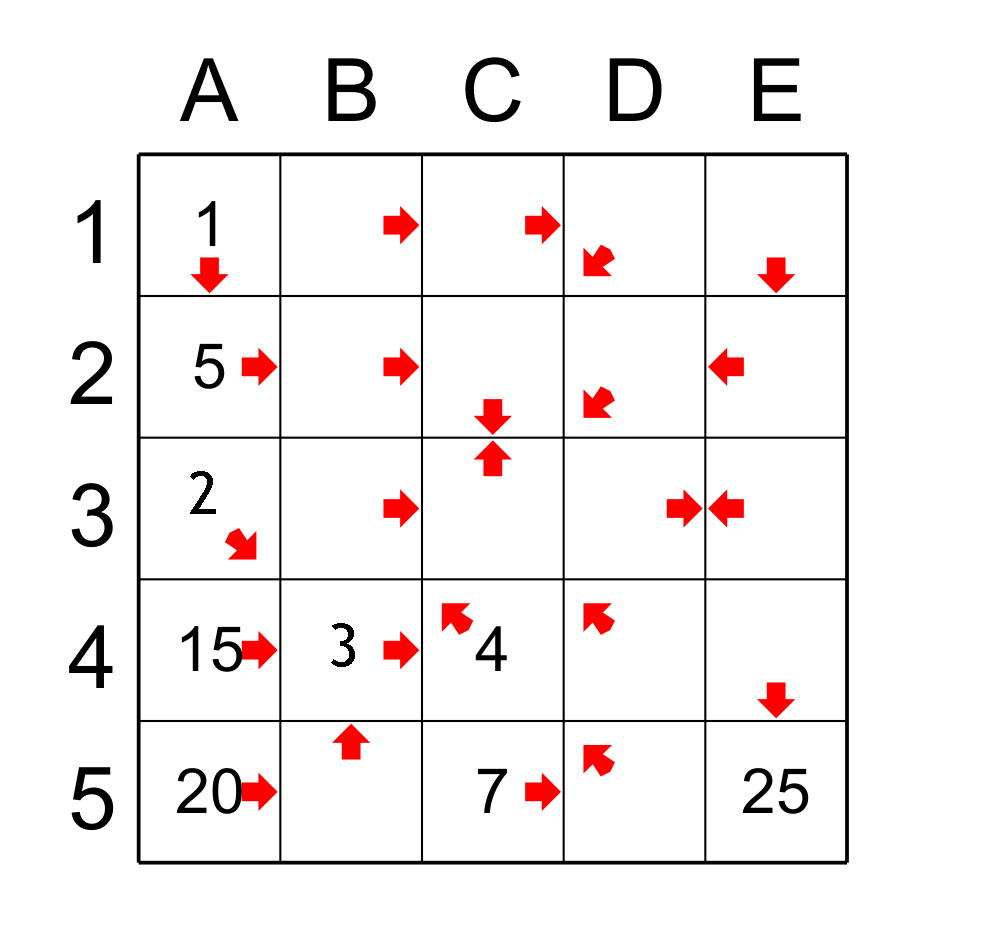
figure 3
Voici l’application du principe du prédécesseur. La case C5 qui a la valeur 7 a trois cases qui pointent vers elle : soit les cases A3 qui a 2, A5 qui a 20 et C2 qui n’a aucune valeur encore. Donc la seule case qui peut être le prédécesseur est la case C2, qui obtient la valeur 6. Nous pouvons appliquer ce raisonnement à la case A5 car il y a seulement une case qui pointe sur elle soit D2, alors D2 aura la valeur 19. Il y a également une seule case qui pointe sur A4 c’est la case D1 alors D1 est le prédécesseur de A4 est a la valeur 14.
La valeur de D5 est 8 car C5 est la seule case qui pointe vers elle avec la valeur 7. Une fois connue la valeur de D5, on trouve la valeur de B3 qui a 9. De plus B5 est le successeur de la case A5 donc B5 a 21. Finalement, la case C5 a une seule est unique case qui pointe vers elle est c'est C2 qui obtient la valeur 6. Figure 4
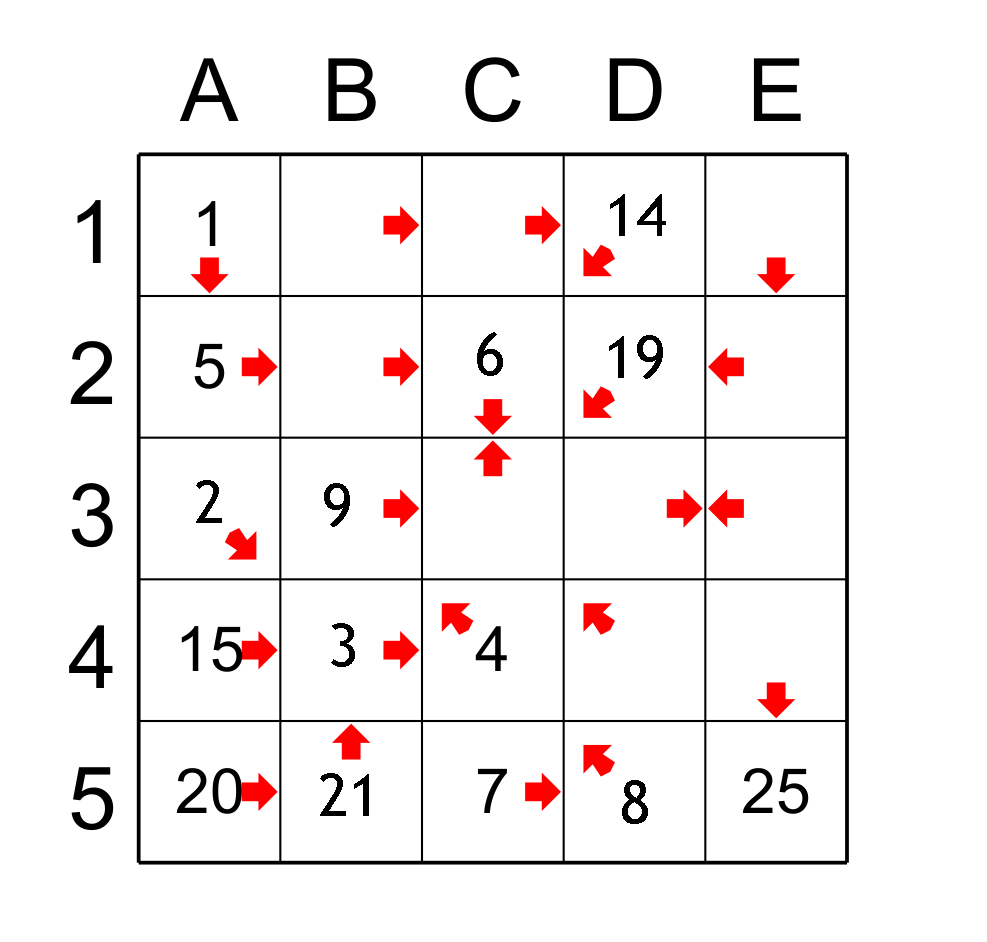
figure 4
Nous pouvons encore trouver des cases avec ces principes: la case E4 pointe uniquement sur E5 donc elle a la valeur 24. Et comme E4 est seulement pointée par la case E1, alors E1 est le prédécesseur avec 23. Nous sommes rendus aux limites de ces deux principes, il nous faut appliquer d'autres raisonnements. Figure 5.
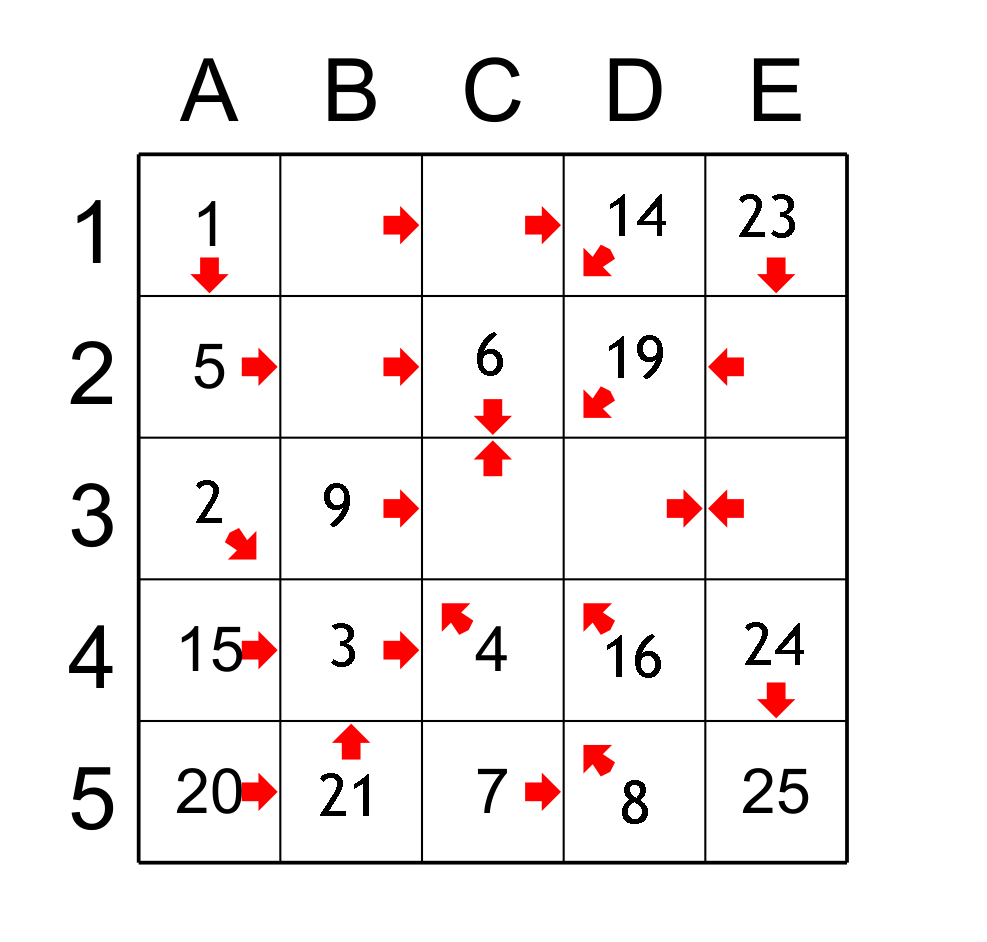
figure 4
Il nous faut touver maintenant les écarts. Nous avons trouvé la séquence de 1 à 9, de 14 à 16, de 19 à 21 et de 23 à 25. Il nous faut donc trouver les trous. C’est souvent plus facile de traiter les écarts les moins grands entre deux séquences. Donc l’écart entre le 21 (B5) et le 23 (E1) est de 1 car il manque le 22 à trouver. Donc il faut trouver une case qui sera le successeur de la case B5 et qui sera en même temps le prédécesseur de la case E1. Seulement la case B1 remplit ce rôle alors B1 obtient la valeur 22.
L’écart suivant le plus petit est entre le 16 (D4) et 19 (D3) qui est de deux, il faut donc trouver les cases qui contiennent 17 et 18. Les seules cases qui peuvent obtenir les valeurs 17 et 18 sont les cases B2 (qui est le successeur de D4) et la case E2 qui est le successeur de B2 et en même temps le prédécesseur de D2. Donc B2 a 17 et E 2 a 19 . Figure 5
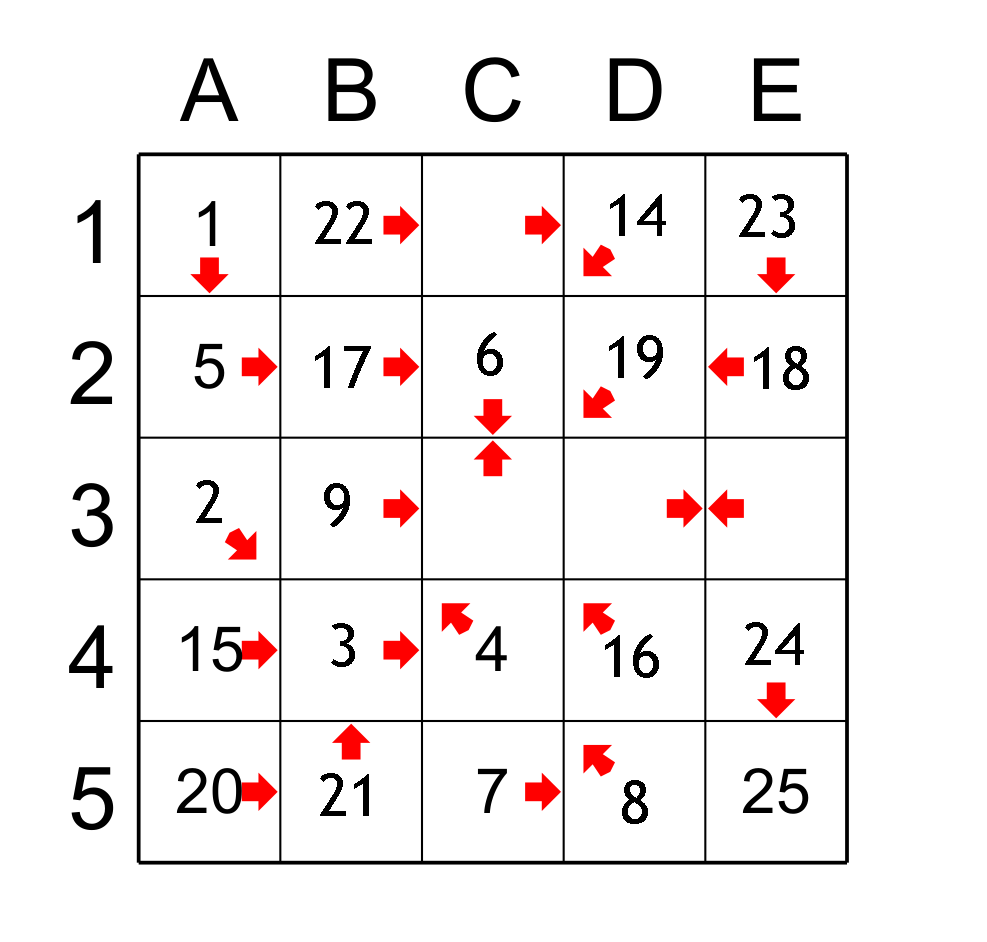
figure 5
Maintenant il reste quatre cases et il faut trouver les valeurs entre 9 et 14 soit 10,11,12 et 13. Il est plus facile de déterminer le prédécesseur de D1 qui est C1 (qui obtient 13) . Ensuite, le prédécesseur de C1 est C3 qui obtient la valeur 12 et le prédécesseur de C3 est E3 (qui a 11) et la dernière case D3 a 10. Voici le jeu est résolu : figure 6.
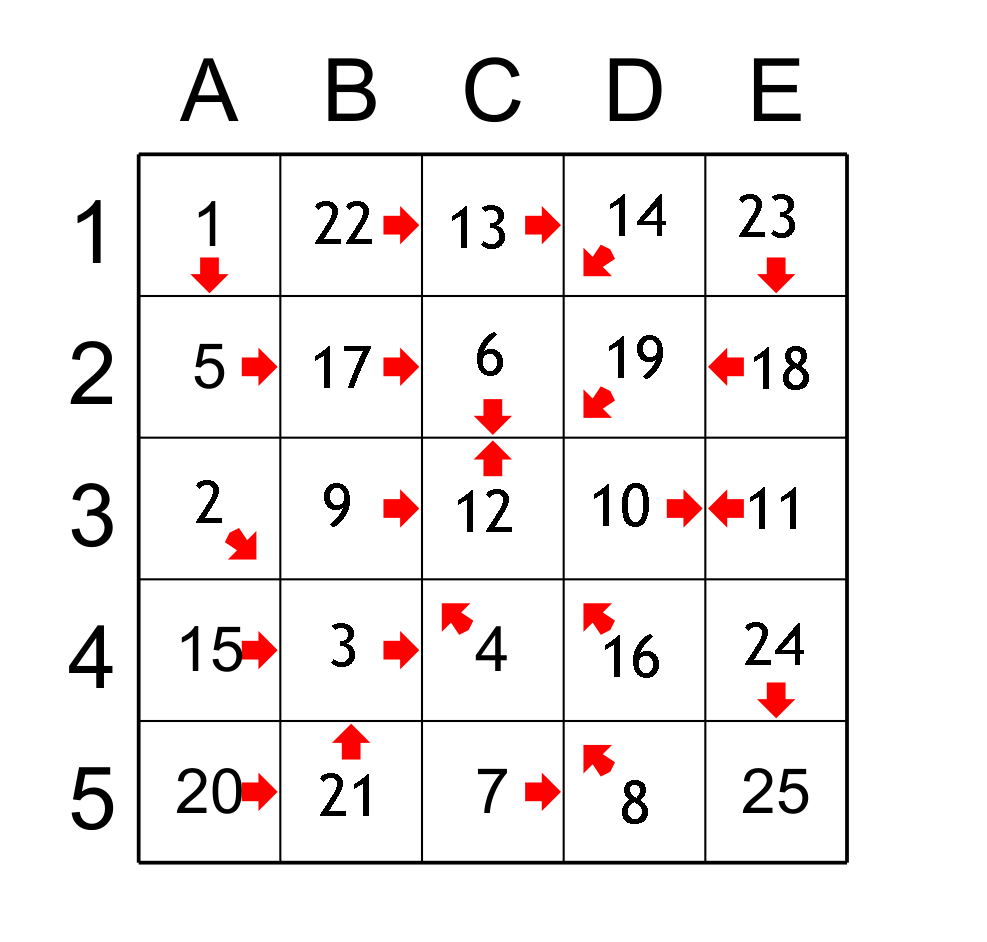
figure 6
Vous découvrirez d’autres techniques de résolution au fur et mesure que vous jouerez.. Vous adorerez.



















Comments powered by CComment