Je vous présente le Flocon Puzzle qui est un jeu fascinant qui est un croisement entre le Sudoku flocon et le kakuro. Il faut être prudent, car on devient vite accro.
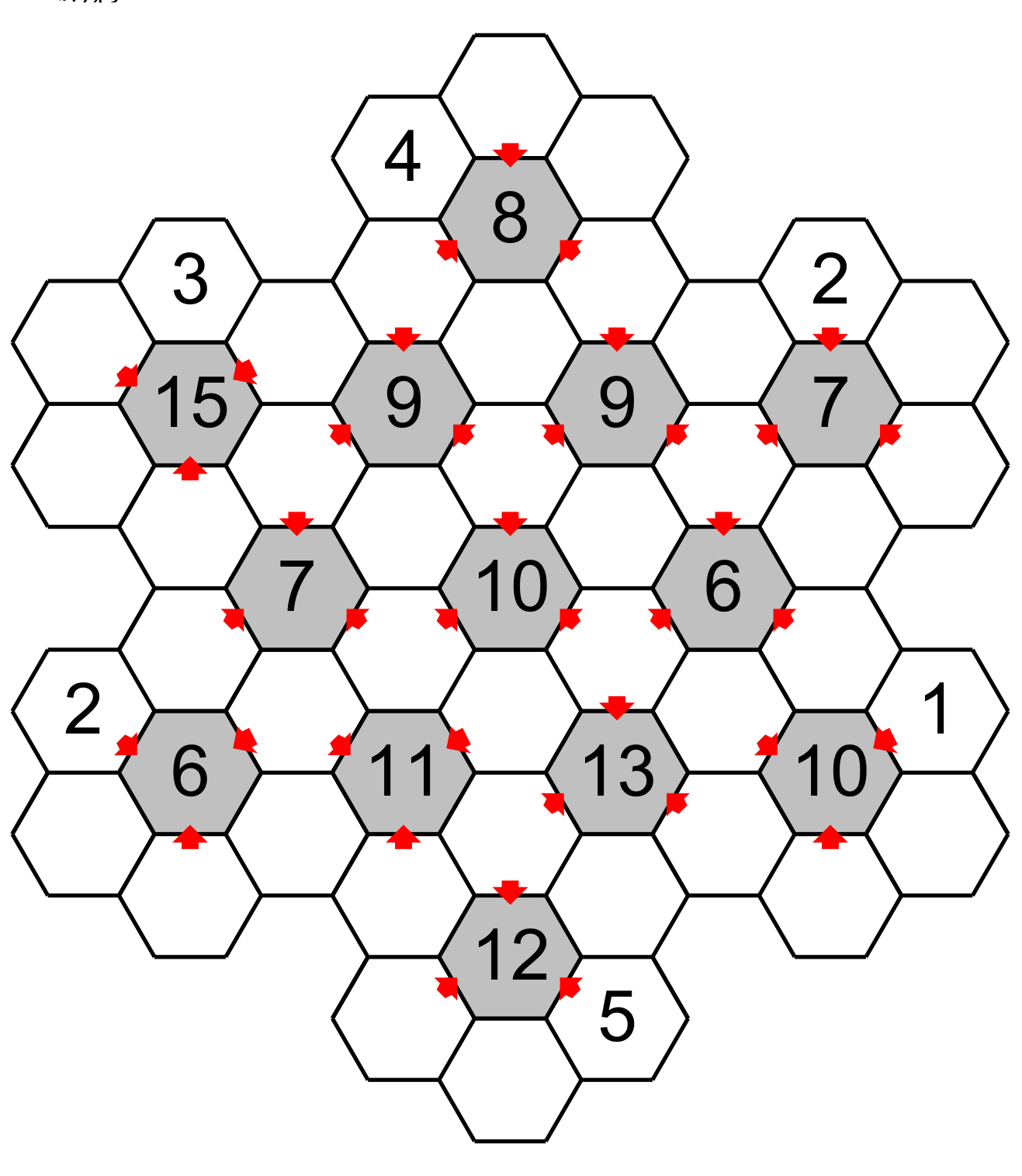
Le Flocon puzzle est avant tout une grille composée de cases hexagonales. Il y a 13 hexagones centraux (en gris) chacun entourés de 6 hexagones vides (en blanc). Les hexagones centraux contiennent la somme des trois hexagones pointant sur eux. Le but du jeu est de trouver les nombres dans les hexagones vides. Chaque hexagone autour d’un hexagone central doit avoir les nombres de 1 à 6, une fois chaque. Au début certaines cases contiennent déjà des nombres. Le but est de trouver tous les nombres manquants. Voici une grille.
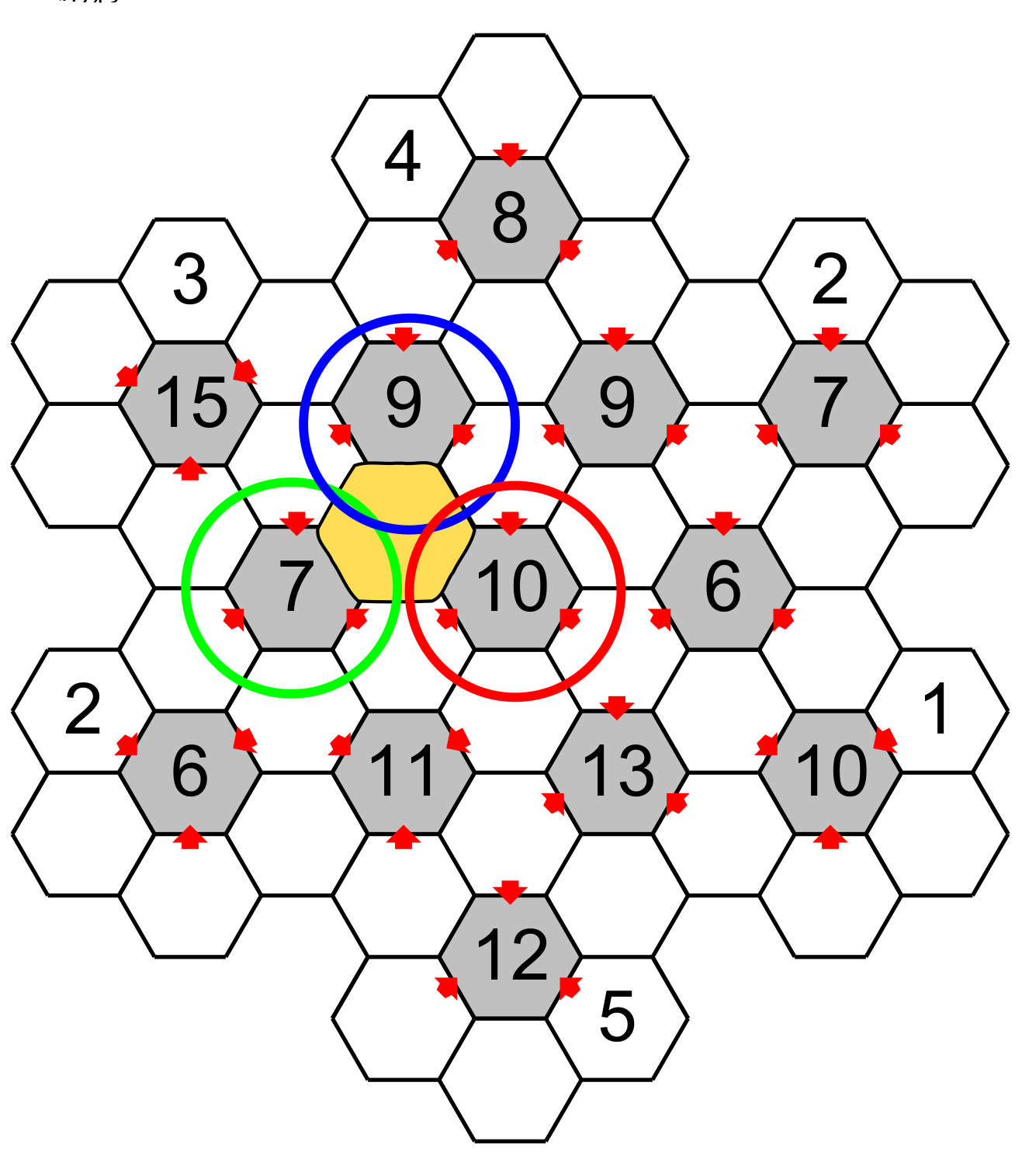
Un hexagone blanc peut être autour d’un, deux ou même trois hexagones centraux, comme le démontre la case en jaune qui est autour de la case centrale 9 (cercle bleu), la case centrale 7 (cercle jaune) et la case 10 (cercle rouge).
Comme tous les hexagones autour d’un hexagone central doivent avoir les nombres 1,2,3,4,5,6 alors le total de toutes les cases autour est de 21 (1+2+3+4+5+6=21. Cela peut nous aider à résoudre la grille. Par exemple, si nous isolons une partie de la grille.
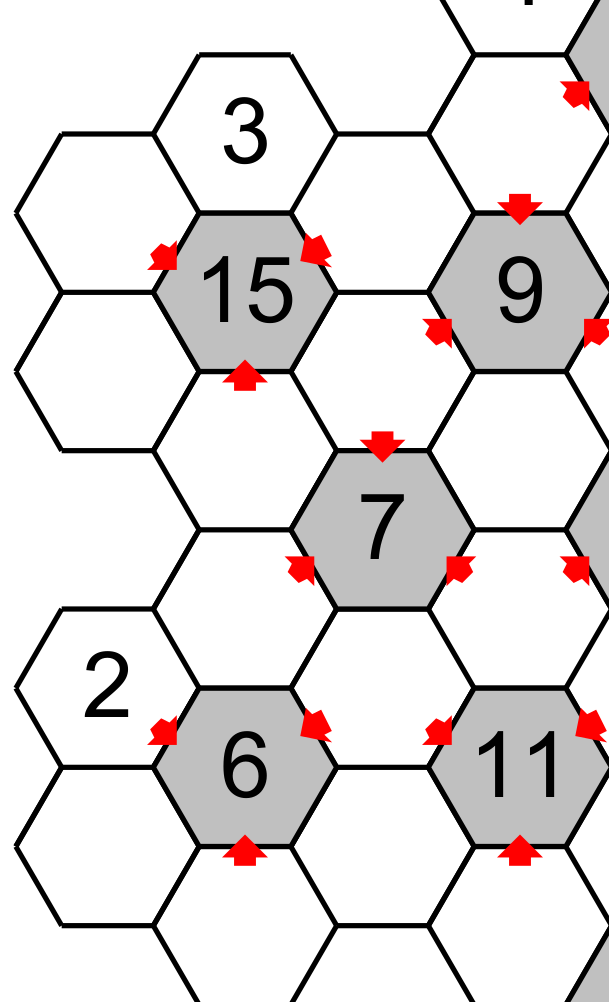
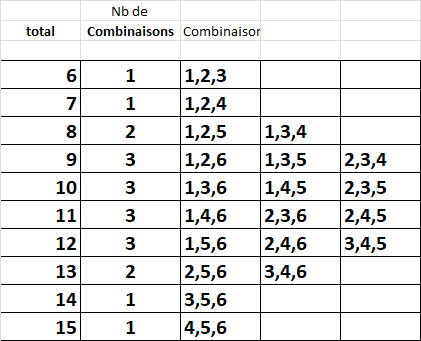
Nous savons que les trois cases qui pointent vers le 15 ont un total de 15. Cela veut dire que les trois autres cases autour du 15 ont un total de 6 (21-15). Il faut savoir que les totaux de 6,7,14 et 15 ont une seule combinaison possible de trois chiffres différents qui donne ces sommes soit : 1+2+3=6,. 1+2+4=7, 3+4+6=14 et 4+5+6=15. Les autres totaux de 8 à 13 peuvent avoir deux ou trois combinaisons différentes (voir la table ci-bas). Donc pour revenir à l’exemple, les cases qui pointent auront les candidats 4,5,6.
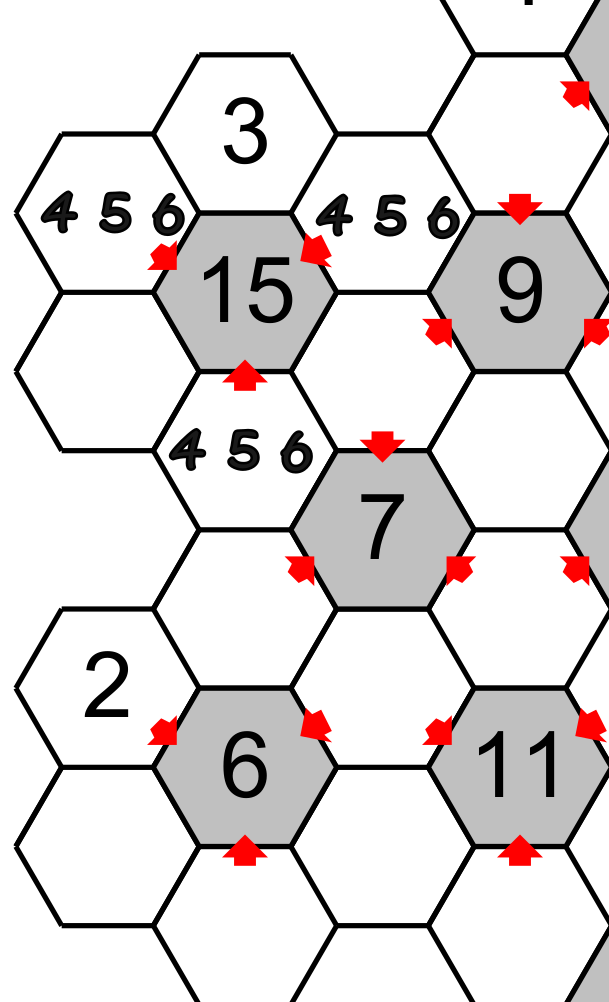
Les autres cases complémentaires ont un total de 6 et aurons 1,2,3 mais comme le 3 est déjà trouvé alors les deux autres cases auront 1 et 2.
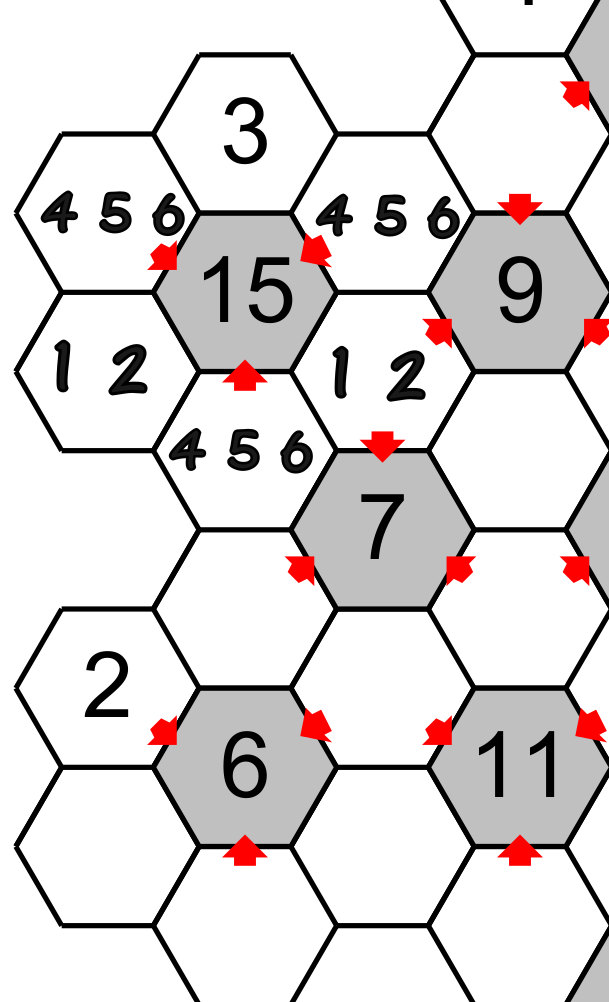
Supposons que plus tard nous trouvons le nombre 2 dans l’hexagone indiqué par le flèche, ce nombre pointe sur le 7 qui a comme unique combinaison de chiffres 1,2 et 4.
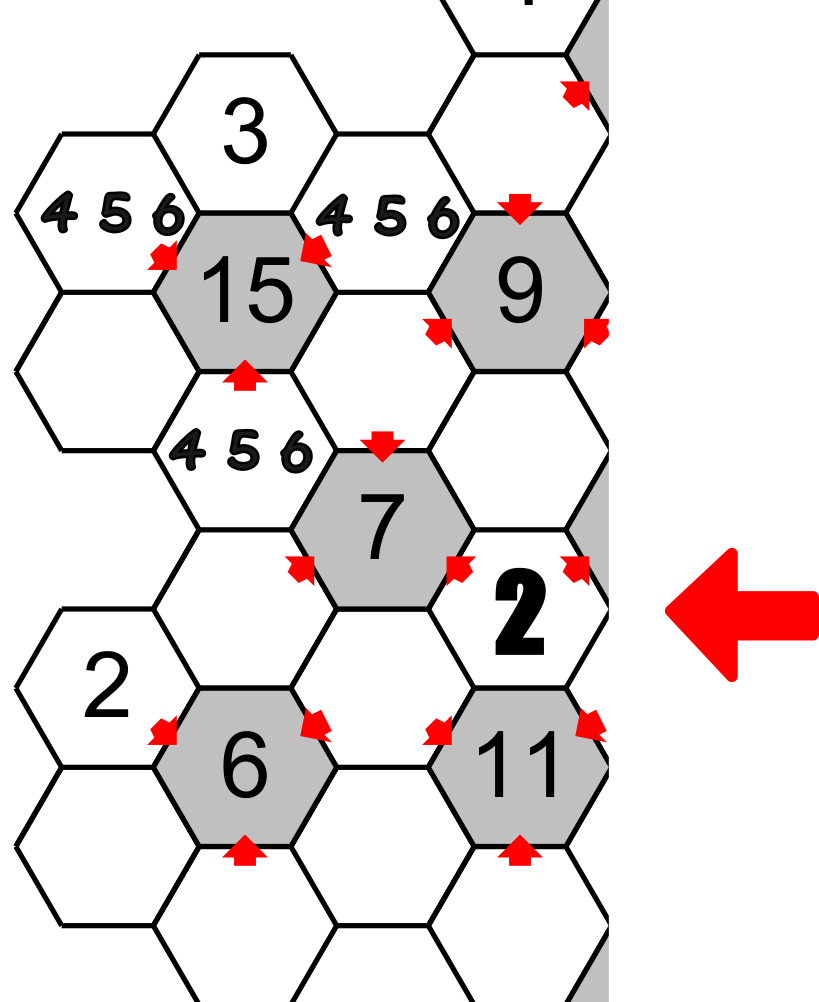
Alors la case située entre le 15, le 9 et le 7, auquel on avait identifié 1 et 2 comme candidats possibles, ne pourra pas avoir le 2, car il est déjà trouvé, alors seul le 1 pourra aller dans cette case. Et par enchainement l’autre case autour du 15 aura le 2 et nous aurons le 4 sous le 7 (rappelez-vous 7=1+2+4) et nous pourrons éliminer le candidat 4 sous le 15.
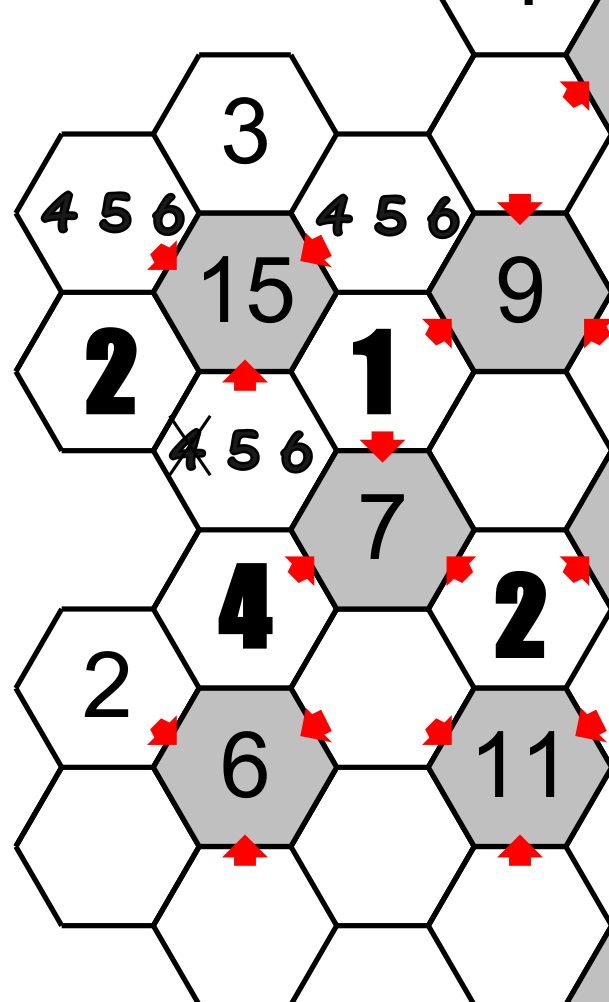
Voilà, il s’agit d’un aperçu comment résoudre ce jeu, n’oubliez pas de vous munir d’une efface.
Voici la table des combinaisons par total.
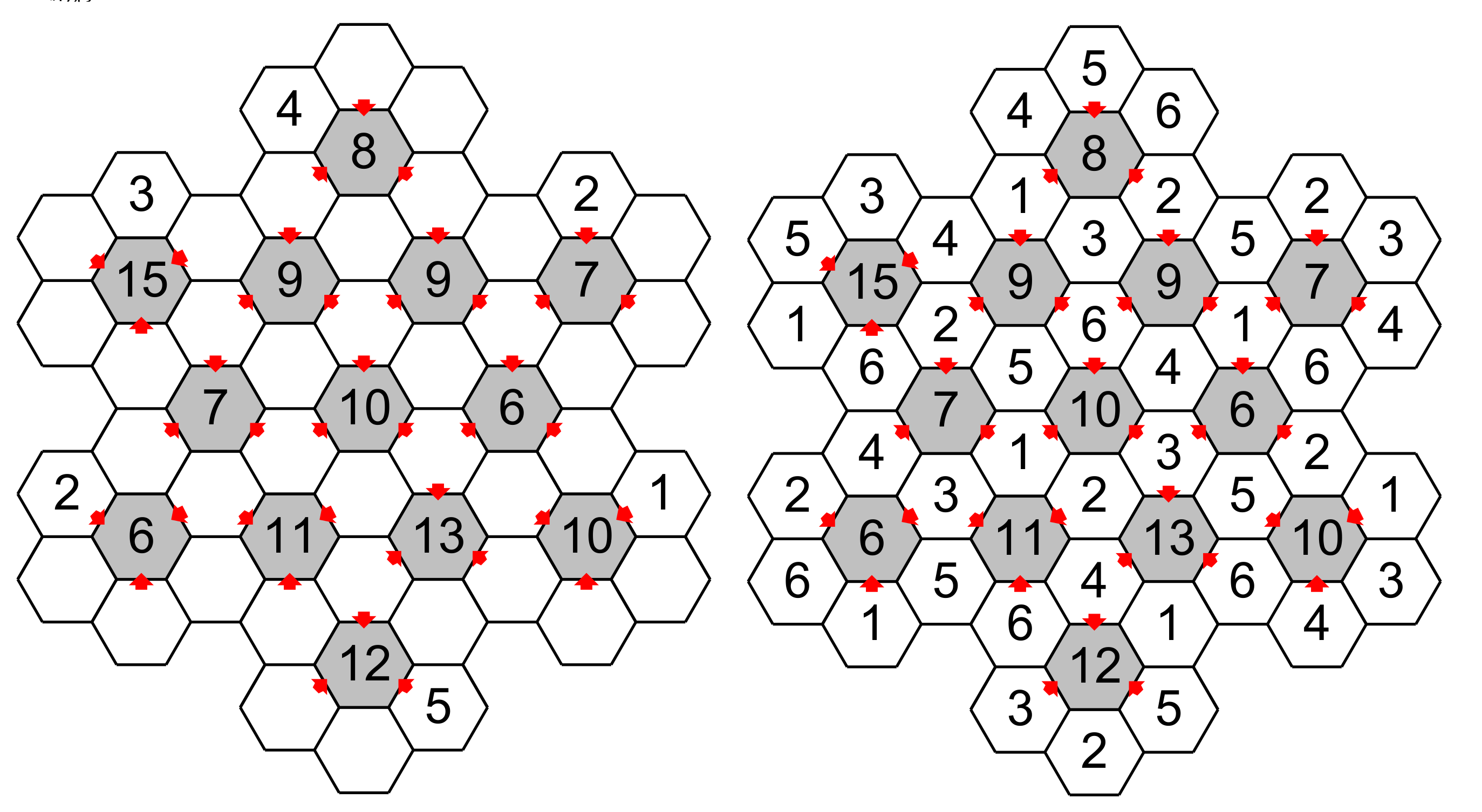
Et voici le jeu et sa solution.
{ccomment on}



















Terms & Conditions
Subscribe
Report
My comments