CHEMIN DE FER
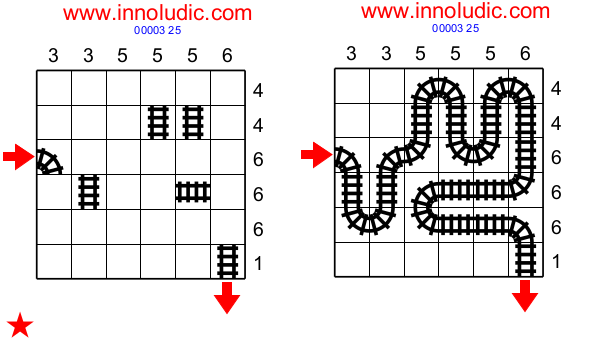
Ce jeu : Le Chemin de Fer aussi appelé "Train Tracks" en anglais est un fascinant jeu de logique aux nombreuses subtilités. Le but est de tracer le chemin que doit emprunter un train pour se rendre d'une flêche à l'autre. Le train se déplace d'une case à l'autre soit en ligne droite (aussi bien vertical qu'horizontal) ou en ligne courbe. Une fois fini, le chemin de fer ne doit jamais se croiser. Il y a déja certains rails qui sont indiqués pour vous aider. De plus les nombres situés aux extremités des colonnes et rangées indiquent le nombre de cases qui contiennent des rails dans les dîtes colonnes ou rangées.
Un des attrait de ce jeux c'est qu'il peut se décliner en plusieurs tailles allant de grilles de 6x6 jusqu'au titanesque grilles de 24x24. De plus j'ai créée des multigrilles qui sont composées de quatre grilles interconnectées.
EXEMPLE DE RESOLUTION
Pour vous donner un apercu de ce jeu je vais résoudre la grille à la figure 1. Pur faciliter la demonstration j'ai ajouté des coordonéées, les colonnes sont identifiées par des chiffres (situé en bas-ne pas confondre avec les indices situés aux haut de la grille) et les rangées par des lettres (A à F) siyuées à droite.
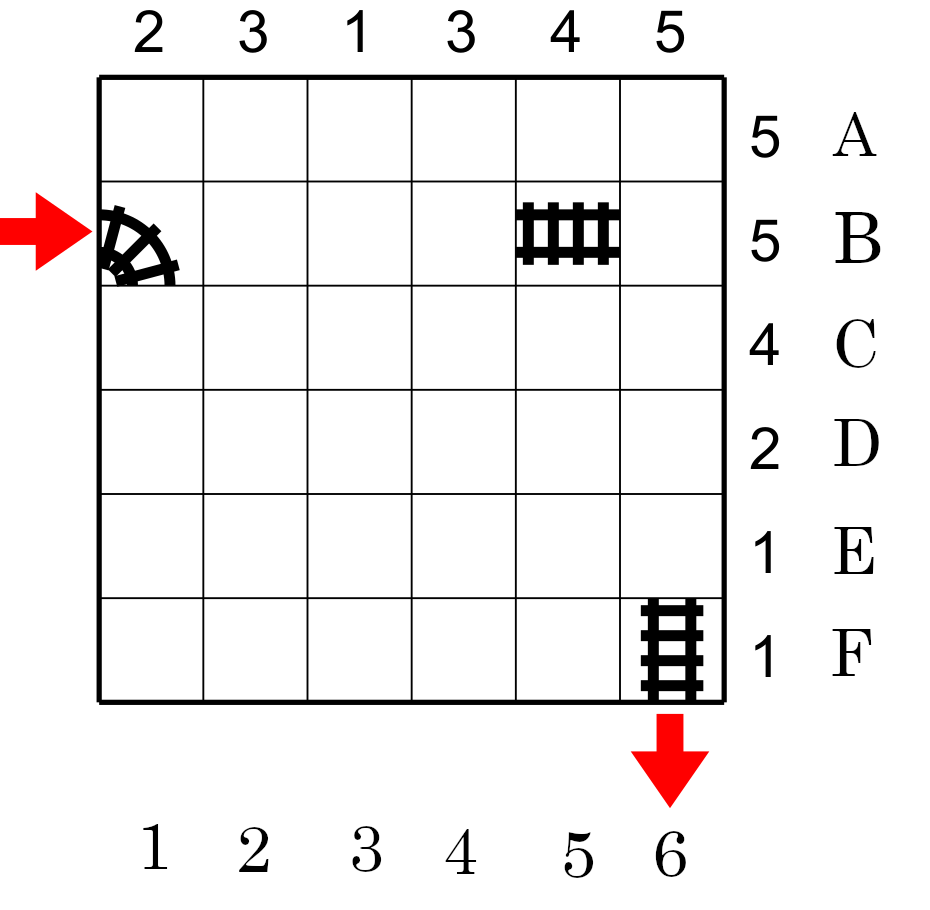
Pour trouver le chemin final, il faut déterminer sur quelles cases celuui-ci passeras e surtout sur quelles cases il ne passeras pas. Il nous faut donc indentifier ces cases.
AU début on peut compléter les rails qui sont déja en place. Le rail B5 continue en B4 et en B6, mais comme nous ne savons pas encore quelle forme elles auront nous pouvons indiquer par un ? ces cases. Lorsque nous aurons plus d,Information plus tard nous pourrons déterminer la nature de ces rails. Le rail en B1 continu en C2, cependant nous avons assez d'information pour savoir que ce rail est courbe, car le nombre de rail que la colonne 1 doit avoir est 2, donc le chemin ne peut continuer sur cette colonne il doit absolument tourner. Nous continuons le rail F6 en F5 avec un ? (voir fig 2)
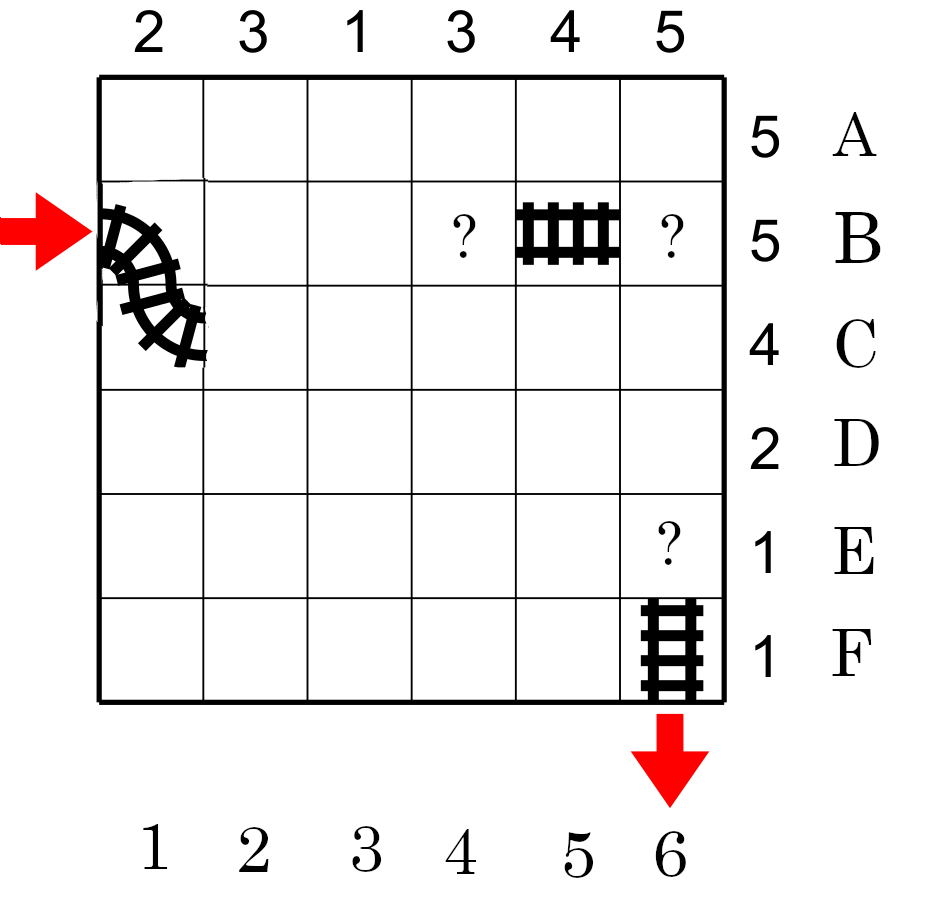
Nous pouvons éliminer des cases où le train ne passeras pas. Comme la colonne 1 a seulement deux cases avec des rails e que ces deux cases sont déja identifiées alors toutes les autres cases peuvent être éliminées. Nous marquons ces cases d'un X. Nous pouvons égalment éliminées les cases vides des rangées F et E avec des X.
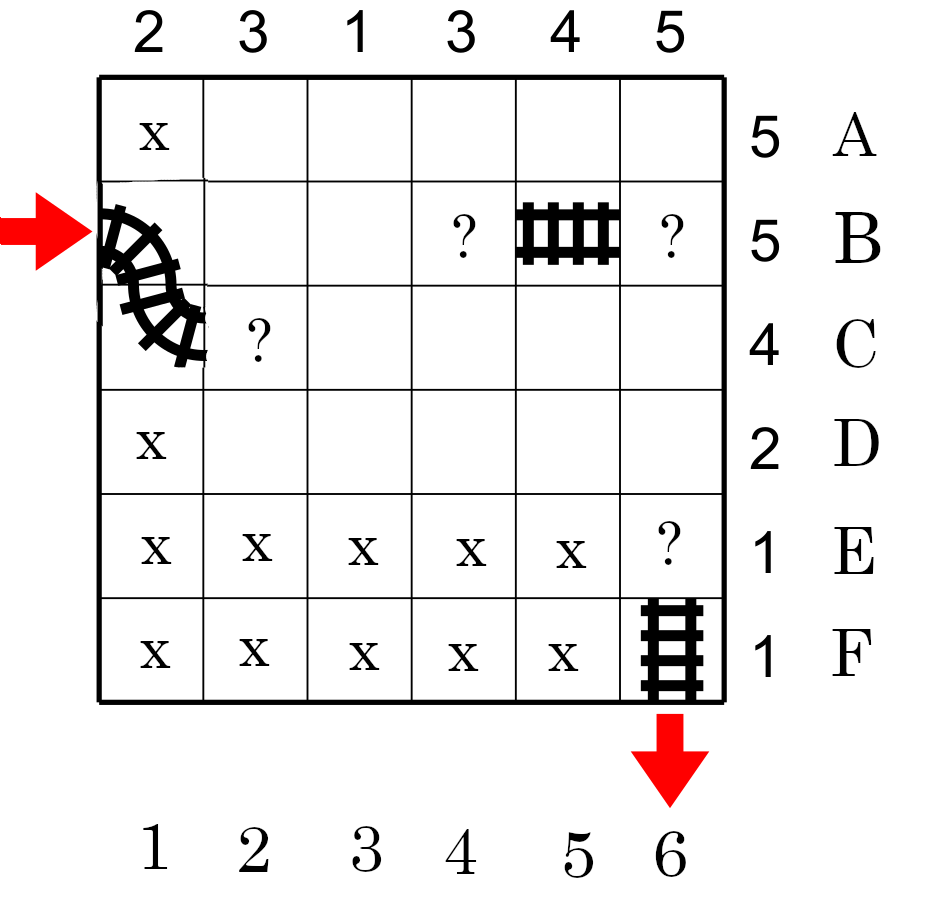
Nous pouvons déterminer que la case E1 doit être droite (Fig. 4).

Comme il ya déja 3 cases vide sur la colonne 5 et qu'il reste 3 cases qui doivent avoir des rails nous pouvons marquer ces cases avec des ? sur la colonne 5. Nous continuons égalment la case E6 en D6 par un ? (Fig. 5).
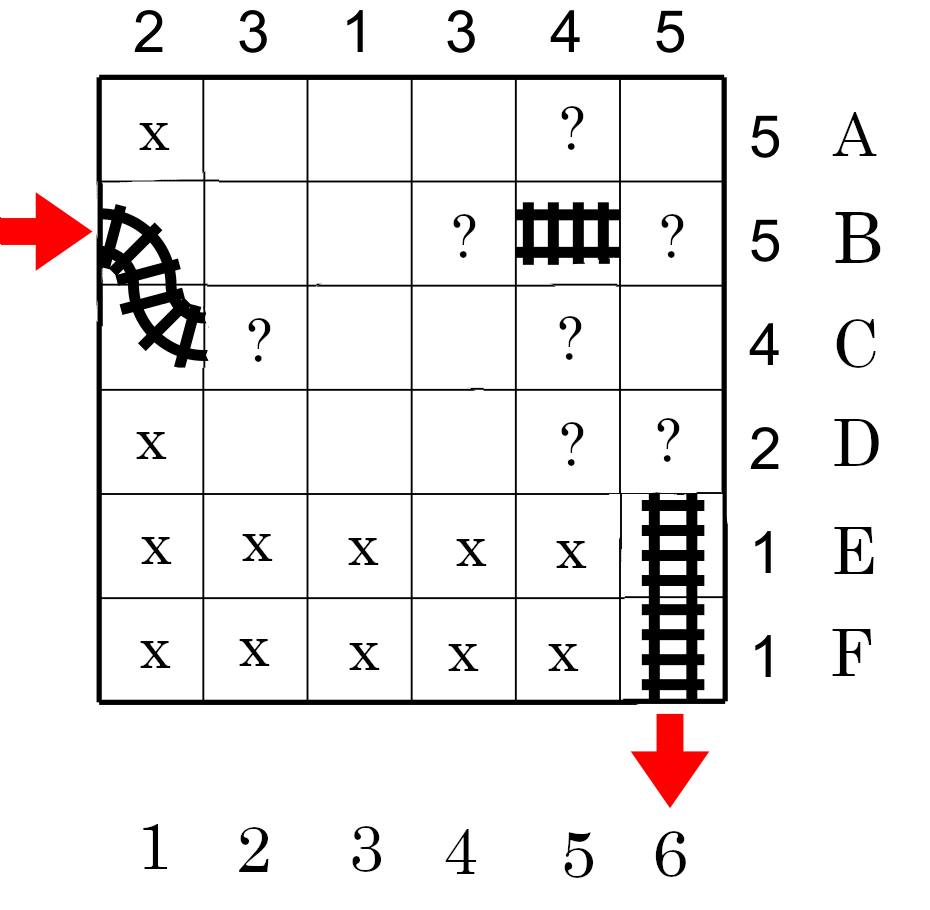
Nous avons assez d'informations pour éliminer les cases vides en marquant de X les cases restantes de la rangée D. Ce qui fait que les cases vides des colonnes 2 et 4 doivent avoir des rails car dans les deux cas il y a deux cases vides et il reste deux cases avec des rails. En appliquant le même raisonnement nous déterminons toutes les cases oû le train passeras (celles avec des ?) voir figure 6.
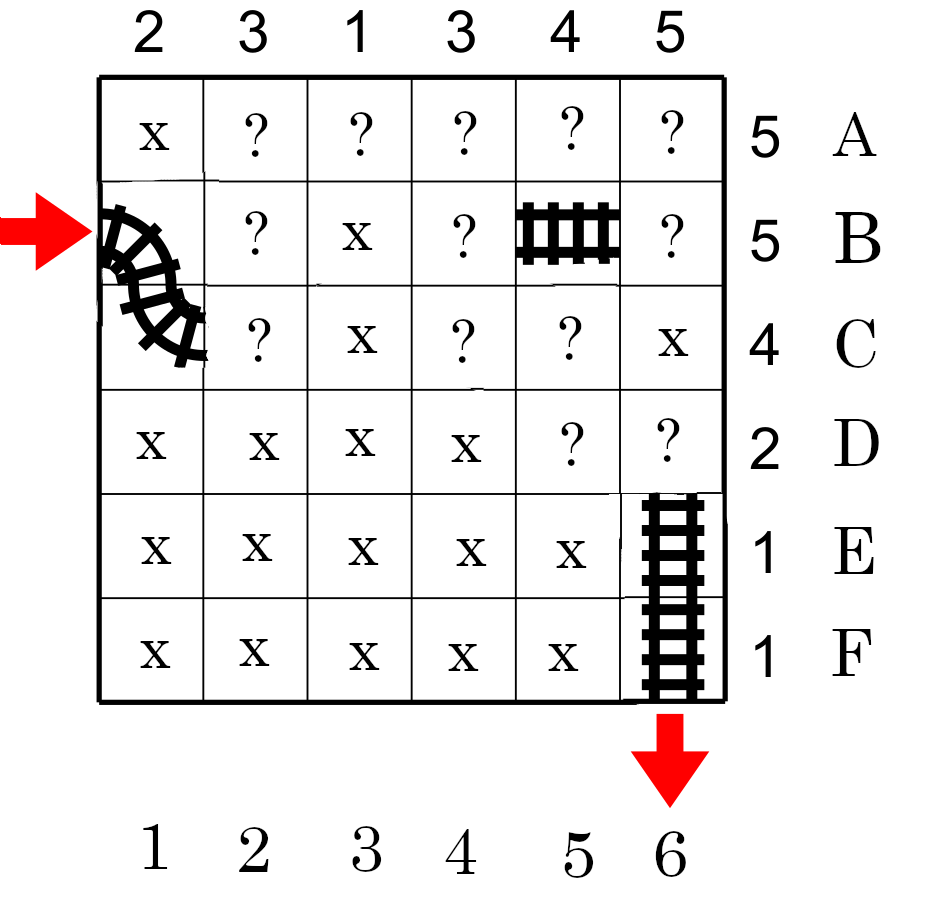
IL devient facile de déterminer que C3 sera courbe et que B3 sera droite et que A3 tourneras. IL suffit d'appliquer ce raissonnment pour identifier le plus possible de rail tout en sachant que le chemin ne doit jamais se croiser. Vous devriez sans trop d'effort arriverà la solution (Fig. 7).
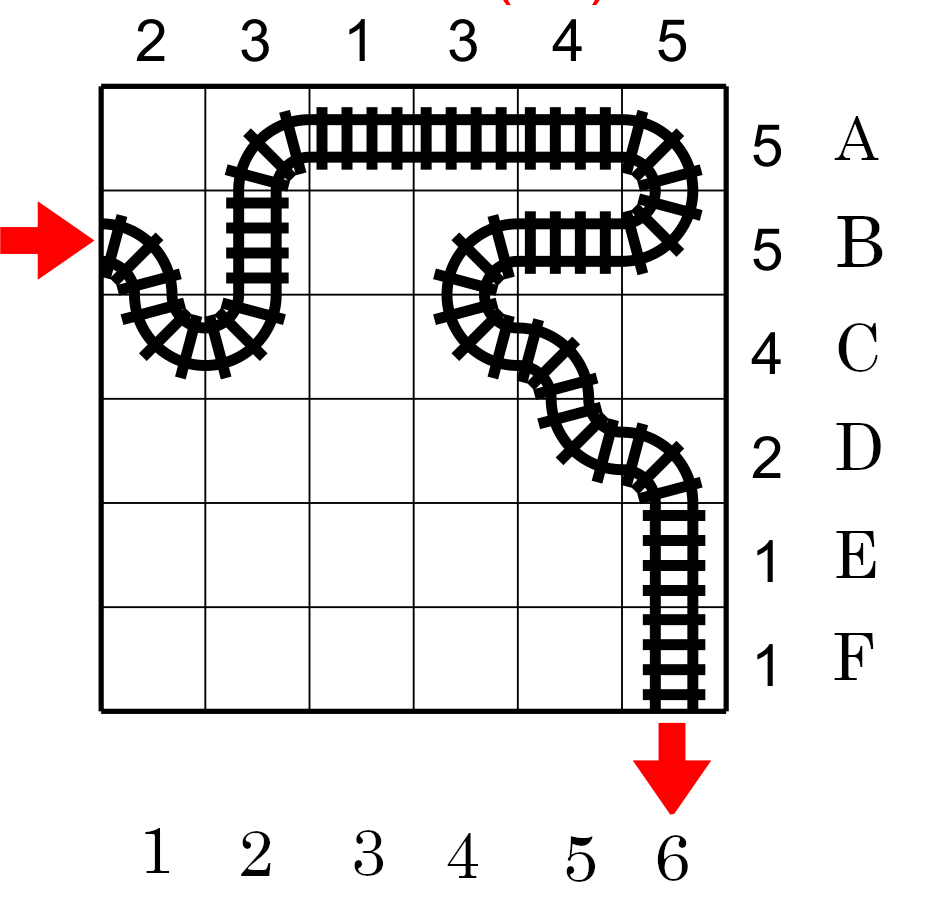
Ce jeu est très facile mais en générale plus la grille est grande plus le niveau est difficile.
MULTIGRILLES
Le multigrille sont composée de quatre grilles reliées ensemble. Le chemin s'établi de grille en grille comme celà.
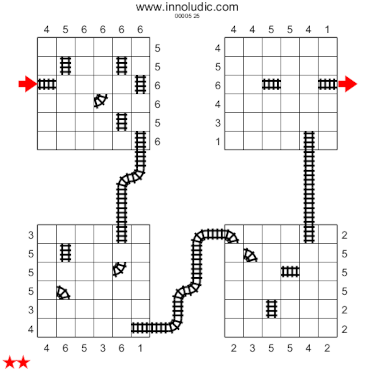
Et voici la solution.

Ces mutigrilles utilisent des grilles 6x6, 8x8 ou 10x10.
Pour mieux apprécier ce jeu il faut prendre place dans le train et l'essayer !
{ccomment on}



















Terms & Conditions
Subscribe
Report
My comments